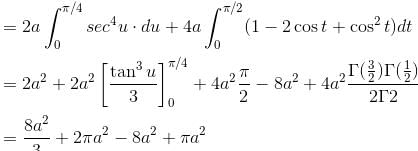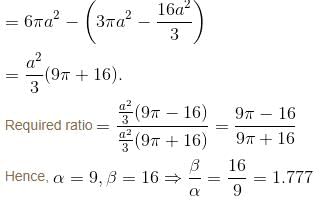Integral Calculus NAT Level - 2 - Physics MCQ
10 Questions MCQ Test - Integral Calculus NAT Level - 2
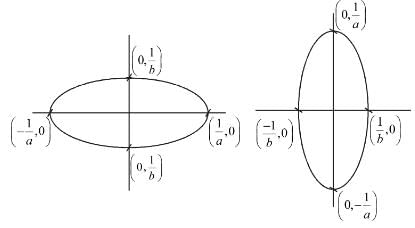
Show that the area common to the ellipses a2x2 + b2y2 = 1, b2x2 + a2y2 = 1. when 0 < a < b is  Find the value of λ.
Find the value of λ.
 Find the value of λ.
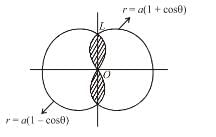
Find the value of λ.If the area shaded in the given figure is of the form λa2. Find the value of λ given the cardioids are r = a(1 + cosθ) and r = a(1 – cosθ) and a given circle r = a.


If ∭R xyz dx dy dz is solved using cylindrical coordinate where R is the region bounded by the planes x = 0, y = 0, z = 0, z = 1 & x2 + y2 = 1 then what is the value of that integral?
Find the area of one loop of the curve 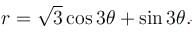 If the area is of the form λπ. Find the value of λ.
If the area is of the form λπ. Find the value of λ.
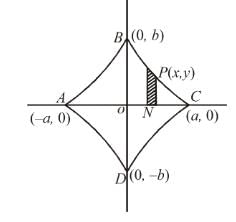
If the whole area of the curve given by the equation x = a cos3 t, y = b sin3 t or 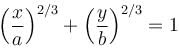 is of the form λπab. Find the value of λ.
is of the form λπab. Find the value of λ.
If the area between the curve x(x2 + y2) = a(x2 – y2) and its asymptote is A1 and the area of the loop is A2 Then value of A1 + A2 = λ·a2. Find the value of λ.
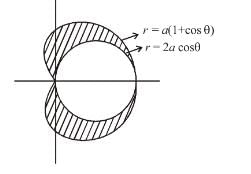
Find the area lying outside the circle r = 2acosθ and inside the cardioid r = a(1 + cosθ). This is of form λπa2. Find value of λ.
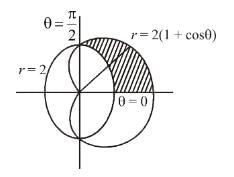
Evaluate  where R is the region in the first quadrant that is outside the circle r = 2 and inside the cardioid r = 2(1 + cosθ).
where R is the region in the first quadrant that is outside the circle r = 2 and inside the cardioid r = 2(1 + cosθ).
If the ratio of the two parts into which the parabola 2a = r(1 + cosθ) divides the area of the cardiod r = 2a(1 + cosθ) is of the form  Find the value of β/α.
Find the value of β/α.



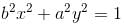



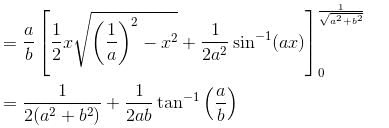
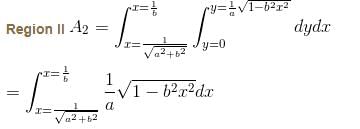
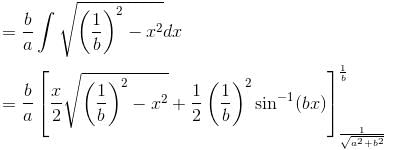

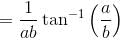
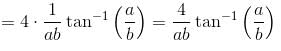



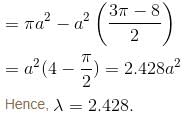

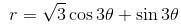
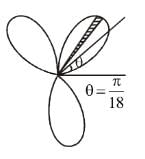

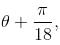 the above equation reduces to r = 2 cos 3θ and the tracing of this curve is as in figure.
the above equation reduces to r = 2 cos 3θ and the tracing of this curve is as in figure.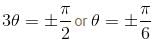 and these is also symmetry about the initial line.
and these is also symmetry about the initial line.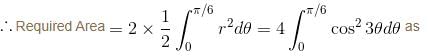
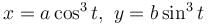

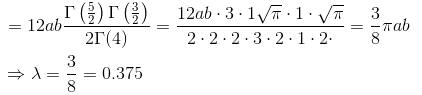



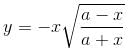
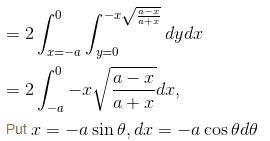
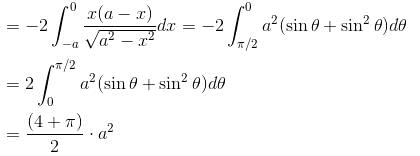
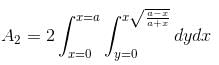


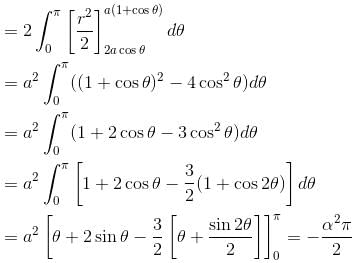

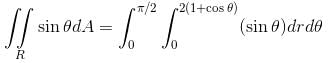
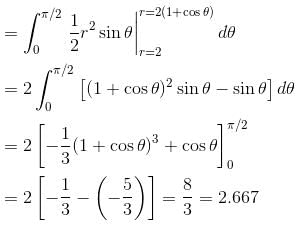
 sin x sin-1 (sin x sin y) dxdy is
sin x sin-1 (sin x sin y) dxdy is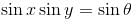
 keeping x constant when
keeping x constant when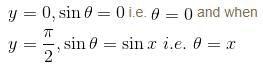
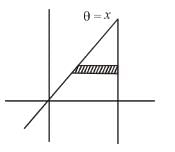

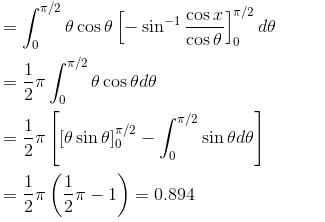

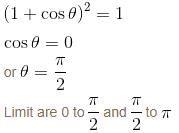

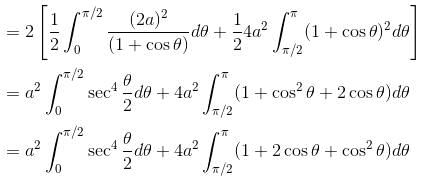
 in the second integral and by putting θ/2 = u in the first integral
in the second integral and by putting θ/2 = u in the first integral