JEE Advanced 2015 Paper -1 with Solutions - JEE MCQ
30 Questions MCQ Test National Level Test Series for JEE Advanced 2025 - JEE Advanced 2015 Paper -1 with Solutions
Section 1
Q. No. 1-8 carry 4 marks each.
The answer to each question is a SINGLE DIGIT INTEGER ranging from 0 to 9, both inclusive.
Q.
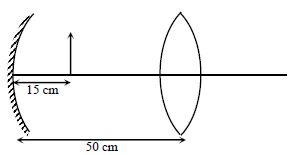
Consider a concave mirror and a convex lens (refractive index = 1.5) of focal length 10 cm each, separated by a distance of 50 cm in air (refractive index = 1) as shown in the figure. An object is placed at a distance of 15 cm from the mirror. Its erect image formed by this combination has magnification M1. When the set- up is kept in a medium of refractive index 7/6, the magnification becomes M2. The magnitude 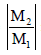 is
is
An infinitely long uniform line charge distribution of charge per unit length λ lies parallel to the y-axis in the
y-z plane at z =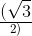 a (see figure). If the magnitude of the flux of the electric field through the rectangular
a (see figure). If the magnitude of the flux of the electric field through the rectangular
surface ABCD lying in the x-y plane with its center at the origin is 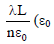 = permittivity of free space), then
= permittivity of free space), then
the value of n is
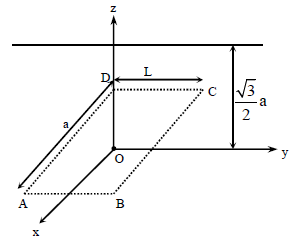
y-z plane at z =
surface ABCD lying in the x-y plane with its center at the origin is
the value of n is
Consider a hydrogen atom with its electron in the nth orbital. An electromagnetic radiation of wavelength
90 nm is used to ionize the atom. If the kinetic energy of the ejected electron is 10.4 eV, then the value of n
is (hc = 1242 eV nm)
90 nm is used to ionize the atom. If the kinetic energy of the ejected electron is 10.4 eV, then the value of n
is (hc = 1242 eV nm)
A bullet is fired vertically upwards with velocity v from the surface of a spherical planet. When it reaches
its maximum height, its acceleration due to the planet’s gravity is 1/4th of its value at the surface of the
planet. If the escape velocity from the planet is , then the value of N is (ignore energy loss due
to atmosphere)
Two identical uniform discs roll without slipping on two different surfaces AB and CD (see figure) starting
at A and C with linear speeds v1 and v2, respectively, and always remain in contact with the surfaces. If
they reach B and D with the same linear speed and v1 = 3 m/s, then v2 in m/s is (g = 10 m/s2)
Two spherical stars A and B emit blackbody radiation. The radius of A is 400 times that of B and A emits
104 times the power emitted from B. The ratio (λA/λB) of their wavelengths λA and λB at which the peaks
occur in their respective radiation curves is
A nuclear power plant supplying electrical power to a village uses a radioactive material of half life T years
as the fuel. The amount of fuel at the beginning is such that the total power requirement of the village is
12.5 % of the electrical power available form the plant at that time. If the plant is able to meet the total
power needs of the village for a maximum period of nT years, then the value of n is
A Young’s double slit interference arrangement with slits S1 and S2 is immersed in water (refractive index = 4/3) as shown in the figure. The positions of maxima on the surface of water are given by x0 = p2m2λ2 – d2, where λ is the wavelength of light in air (refractive index = 1), 2d is the separation between the slits and m is an integer. The value of p is
Section 2
Q. No. 9 - 18 carry 4 marks each and 2 marks is deducted for every wrong answer.
Each question has FOUR options (A), (B), (C) and (D). ONE OR MORE THAN ONE of these four
option(s) is(are) correct.
Q.
For photo-electric effect with incident photon wavelength λ, the stopping potential is V0. Identify the
correct variation(s) of V0 with λ and 1/λ
Consider a Vernier callipers in which each 1 cm on the main scale is divided into 8 equal divisions and a
screw gauge with 100 divisions on its circular scale. In the Vernier callipers, 5 divisions of the Vernier
scale coincide with 4 divisions on the main scale and in the screw gauge, one complete rotation of the
circular scale moves it by two divisions on the linear scale. Then:
Planck’s constant h, speed of light c and gravitational constant G are used to form a unit of length L and a
unit of mass M. Then the correct option(s) is(are)
Two independent harmonic oscillators of equal mass are oscillating about the origin with angular
frequencies ω1 and ω2 and have total energies E1 and E2, respectively. The variations of their momenta p
with positions x are shown in the figures. If a/b =n2 and a/R =n, then the correct equation(s) is(are)
A ring of mass M and radius R is rotating with angular speed ω about a fixed vertical axis passing through its centre O with two point masses each of mass M/8 at rest at O. These masses can move radially outwards along two massless rods fixed on the ring as shown in the figure. At some instant the angular speed
of the system is 8/9 ω and one of the masses is at a distance of 3/5 R from O. At this instant the distance of the other mass from O is
The figures below depict two situations in which two infinitely long static line charges of constant positive
line charge density λ are kept parallel to each other. In their resulting electric field, point charges q and -q
are kept in equilibrium between them. The point charges are confined to move in the x direction only. If
they are given a small displacement about their equilibrium positions, then the correct statement(s) is(are)
Two identical glass rods S1 and S2 (refractive index = 1.5) have one convex end of radius of
curvature 10 cm. They are placed with the curved surfaces at a distance d as shown in the figure, with their axes (shown by the dashed line) aligned. When a point source of light P is placed inside rod S1 on its axis at a distance of 50 cm from the curved face, the light rays emanating from it are found to be parallel to the axis inside S2. The distance d is
A conductor (shown in the figure) carrying constant current I is kept in the x-y plane in a uniform magnetic
field If F is the magnitude of the total magnetic force acting on the conductor, then the correct
statement(s) is(are)
A container of fixed volume has a mixture of one mole of hydrogen and one mole of helium in equilibrium
at temperature T. Assuming the gases are ideal, the correct statement(s) is(are)
In an aluminium (Al) bar of square cross section, a square hole is drilled and is filled with iron (Fe) as
shown in the figure. The electrical resistivities of Al and Fe are 2.7 × 10–8 m and 1.0 × 10–7
m,
respectively. The electrical resistance between the two faces P and Q of the composite bar is
SECTION 3
Q. No. 19 -20 carry 2 marks each and 1 mark is deducted for every wrong answer.
Each question contains two columns, Column I and Column II
Column I has four entries (A), (B), (C) and (D)
Column II has five entries (P), (Q), (R), (S) and (T)
Match the entries in Column I with the entries in Column II
Q.
Match the nuclear processes given in column I with the appropriate option(s) in column II
A particle of unit mass is moving along the x-axis under the influence of a force and its total energy is
conserved. Four possible forms of the potential energy of the particle are given in column I (a and U0 are
constants). Match the potential energies in column I to the corresponding statement(s) in column II.
SECTION – 1
Q. No. - 21 - 28 carry 4 marks each.
The answer to each question is a SINGLE DIGIT INTEGER ranging from 0 to 9, both inclusive
Q.
If the freezing point of a 0.01 molal aqueous solution of a cobalt (III) chloride-ammonia complex(which
behaves as a strong electrolyte) is – 0.05580C, the number of chloride(s) in the coordination sphere of the
complex is
[Kf of water = 1.86 K kg mol–1]
The total number of stereoisomers that can exist for M is
The number of resonance structures for N is
The total number of lone pairs of electrons in N2O3 is
For the octahedral complexes of Fe3+ in SCN– (thiocyanato-S) and in CN– ligand environments, the
difference between the spin-only magnetic moments in Bohr magnetons (When approximated to the nearest
integer) is
[Atomic number of Fe = 26]
Among the triatomic molecules/ions the total
number of linear molecule(s)/ion(s) where the hybridization of the central atom does not have contribution
from the d-orbital(s) is
[Atomic number: S = 16, Cl = 17, I = 53 and Xe = 54]
Not considering the electronic spin, the degeneracy of the second excited state( n = 3) of H atom is 9, while
the degeneracy of the second excited state of H– is
All the energy released from the reaction
is used for oxidizing
Under standard conditions, the number of moles of M+ oxidized when one mole of X is converted to Y is
[F = 96500 C mol–1]
SECTION 2
Q. No 29 - 38 carry 4 marks each and 2 marks are deducted for every wrong answer.
Each question has FOUR options (A), (B), (C) and (D). ONE OR MORE THAN ONE of these four
option(s) is(are) correct.
Q.
If the unit cell of a mineral has cubic close packed (ccp) array of oxygen atoms with m fraction of
octahedral holes occupied by aluminium ions and n fraction of tetrahedral holes occupied by magnesium
ions, m and n, respectively, are
Compound(s) that on hydrogenation produce(s) optically inactive compound(s) is (are)
|
3 videos|2 docs|40 tests
|
|
3 videos|2 docs|40 tests
|




















