JEE Advanced 2015 Paper -2 with Solutions - JEE MCQ
30 Questions MCQ Test National Level Test Series for JEE Advanced 2025 - JEE Advanced 2015 Paper -2 with Solutions
Section 1
Q. No. 1 - 8 Carry 4 marks each
The answer to each question is a SINGLE DIGIT INTEGER ranging from 0 to 9, both inclusive.
Q.
An electron in an excited state of Li2+ ion has angular momentum 3h/2π. The de Broglie wavelength of the
electron in this state is pπa0 (where a0 is the Bohr radius). The value of p is
electron in this state is pπa0 (where a0 is the Bohr radius). The value of p is
A large spherical mass M is fixed at one position and two identical point masses m are kept on a line
passing through the centre of M (see figure). The point masses are connected by a rigid massless rod of
length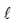 
and this assembly is free to move along the line connecting them. All three masses interact only
through their mutual gravitational interaction. When the point mass nearer to M is at a distance r = 3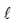 from
M, the tension in the rod is zero for m = k(M/288). The value of k is
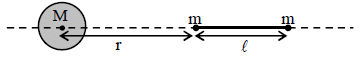
passing through the centre of M (see figure). The point masses are connected by a rigid massless rod of
length
and this assembly is free to move along the line connecting them. All three masses interact onlythrough their mutual gravitational interaction. When the point mass nearer to M is at a distance r = 3
fromM, the tension in the rod is zero for m = k(M/288). The value of k is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The energy of a system as a function of time t is given as E(t) = A2exp(-αt), where α = 0.2 s-1. The
measurement of A has an error of 1.25 %. If the error in the measurement of time is 1.50 %, the percentage
error in the value of E(t) at t = 5 s is
measurement of A has an error of 1.25 %. If the error in the measurement of time is 1.50 %, the percentage
error in the value of E(t) at t = 5 s is
The densities of two solid spheres A and B of the same radii R vary with radial distance r as ρA(r) =
, respectively, where k is a constant. The moments of inertia of the individual spheres about axes passing through their centres are IA and IB, respectively. If 
the value of n is
Four harmonic waves of equal frequencies and equal intensities I0 have phase angles 0, π/3, 2π/3 and π.
When they are superposed, the intensity of the resulting wave is nI0. The value of n is
For a radioactive material, its activity A and rate of change of its activity R are defined as 
and 
, where N(t) is the number of nuclei at time t. Two radioactive sources P (mean life 
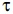) and
Q(mean life 2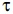) have the same activity at t = 0. Their rates of change of activities at t = 2 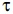are RP and RQ,
respectively. If 
, then the value of n is
A monochromatic beam of light is incident at 600 on one face of an equilateral prism of refractive index n and
emerges from the opposite face making an angle θ(n) with the normal (see the figure). For n = √3 the value of θ is 600 and 
. The value of m is
In the following circuit, the current through the resistor R (=2
) is I Amperes. The value of I is
Section 2
Q. No. 9 -18 carry 4 marks each and 2 marks is deducted for every wrong answer.
Each question has FOUR options (A), (B), (C) and (D). ONE OR MORE THAN ONE of these four
option(s) is(are) correct.
Q.
A fission reaction is given by 
where x and y are two particles. Considering 
to be at rest, the kinetic energies of the products are denoted by KXe, KSr, Kx(2MeV) and Ky(2MeV),
respectively. Let the binding energies per nucleon of 
be 7.5 MeV, 8.5 MeV and 8.5 MeV respectively. Considering different conservation laws, the correct option(s) is(are)
Two spheres P and Q of equal radii have densities ρ1 and ρ2, respectively. The spheres are connected by a massless string and placed in liquids L1 and L2 of densities σ1 and σ2 and viscosities η1 and
η2, respectively. They float in equilibrium with the sphere P in L1 and sphere Q in L2 and the string being taut (see figure). If sphere P alone in L2 has terminal velocity 
and Q alone in L1 has terminal velocity 
,
ρ then
In terms of potential difference V, electric current I, permittivity ε0, permeability μ0 and speed of light c,
the dimensionally correct equation(s) is(are)
Consider a uniform spherical charge distribution of radius R1 centred at the origin O. In this distribution, a spherical cavity of radius R2, centred at P with distance OP = a = R1 – R2 (see figure) is made. If the electric field inside the cavity at position 
then the correct statement(s) is(are)
In plotting stress versus strain curves for two materials P and Q, a student by mistake puts strain on the y-axis and stress on the x-axis as shown in the figure. Then the correct statement(s) is(are)
A spherical body of radius R consists of a fluid of constant density and is in equilibrium under its own
gravity. If P(r) is the pressure at r(r < R), then the correct option(s) is(are)
parallel plate capacitor having plates of area S and plate separation d, has capacitance C1 in air. When
two dielectrics of different relative permittivities (ε1 = 2 and ε2 = 4) are introduced between the two plates
as shown in the figure, the capacitance becomes C2. The ratio C2/C1 is
An ideal monoatomic gas is confined in a horizontal cylinder by a spring loaded piston (as shown in the
figure). Initially the gas is at temperature T1, pressure P1 and volume V1 and the spring is in its relaxed state.
The gas is then heated very slowly to temperature T2, pressure P2 and volume V2. During this process the
piston moves out by a distance x. Ignoring the friction between the piston and the cylinder, the correct
statement(s) is(are)
SECTION 3
Q. No. 17-20 carry 4 marks each and 2 marks is deducted for every wrong answer.
This section contains TWO paragraphs
Based on each paragraph, there will be TWO questions
Each question has FOUR options (A), (B), (C) and (D). ONE OR MORE THAN ONE of these four
option(s) is(are) correct
PARAGRAPH 1
Light guidance in an optical fiber can be understood by considering a structure comprising of thin solid glass cylinder of refractive index n1 surrounded by a medium of lower refractive index n2. The light guidance in the structure takes place due to successive total internal reflections at the interface of the media n1 and n2 as shown in the figure. All rays with the angle of incidence i less than a particular value im are confined in the medium of refractive index n1. The numerical aperture (NA) of the structure is defined as sin im.
Q.
For two structures namely S1 with n1 = 
and n2= 3 / 2, and S2 with n1 = 8/5 and n2 = 7/5 and
taking the refractive index of water to be 4/3 and that of air to be 1, the correct option(s) is(are)
PARAGRAPH 1
Light guidance in an optical fiber can be understood by considering a structure comprising of thin solid glass cylinder of refractive index n1 surrounded by a medium of lower refractive index n2. The light guidance in the structure takes place due to successive total internal reflections at the interface of the media n1 and n2 as shown in the figure. All rays with the angle of incidence i less than a particular value im are confined in the medium of refractive index n1. The numerical aperture (NA) of the structure is defined as sin im.
Q.
If two structures of same cross-sectional area, but different numerical apertures NA1 and
NA2 (NA2 < NA1 ) are joined longitudinally, the numerical aperture of the combined structure is
PARAGRAPH 2
In a thin rectangular metallic strip a constant current I flows along the positive x-direction, as shown in the figure. The length, width and thickness of the strip are 
, w and d, respectively. A uniform magnetic field 
is applied on the strip along the positive y-direction. Due to this, the charge carriers experience a net deflection along the zdirection. This results in accumulation of charge carriers on the surface PQRS and appearance of equal and opposite charges on the face opposite to PQRS. A potential difference along the z-direction is thus developed. Charge accumulation continues until the magnetic force is balanced by the electric force. The current is assumed to be uniformly distributed on the cross section of the strip and carried by electrons.
Q.
Consider two different metallic strips (1 and 2) of the same material. Their lengths are the same, widths are
w1 and w2 and thicknesses are d1 and d2, respectively. Two points K and M are symmetrically located on
the opposite faces parallel to the x-y plane (see figure). V1 and V2 are the potential differences between K
and M in strips 1 and 2, respectively. Then, for a given current I flowing through them in a given magnetic
field strength B, the correct statement(s) is(are)
PARAGRAPH 2
In a thin rectangular metallic strip a constant current I flows along the positive x-direction, as shown in the figure. The length, width and thickness of the strip are , w and d, respectively. A uniform magnetic field is applied on the strip along the positive y-direction. Due to this, the charge carriers experience a net deflection along the zdirection. This results in accumulation of charge carriers on the surface PQRS and appearance of equal and opposite charges on the face opposite to PQRS. A potential difference along the z-direction is thus developed. Charge accumulation continues until the magnetic force is balanced by the electric force. The current is assumed to be uniformly distributed on the cross section of the strip and carried by electrons.
Q.
Consider two different metallic strips (1 and 2) of same dimensions (lengths , width w and thickness d)
with carrier densities n1 and n2, respectively. Strip 1 is placed in magnetic field B1 and strip 2 is placed in
magnetic field B2, both along positive y-directions. Then V1 and V2 are the potential differences developed
between K and M in strips 1 and 2, respectively. Assuming that the current I is the same for both the strips,
the correct option(s) is(are)
SECTION 1
Q. No. 21 -28 carry 4 marks each.
The answer to each question is a SINGLE DIGIT INTEGER ranging from 0 to 9, both inclusive
Q.
In dilute aqueous H2SO4, the complex diaquodioxalatoferrate(II) is oxidized by 
. For this reaction, the ratio of the rate of change of [H+] to the rate of change of 
is
The number of hydroxyl group(s) in Q is
Among the following, the number of reaction(s) that produce(s) benzaldehyde is
In the complex acetylbromidodicarbonylbis(triethylphosphine)iron(II), the number of Fe–C bond(s) is
Among the complex ions, 
number of complex
ion(s) that show(s) cis-trans isomerism is
Three moles of B2H6 are completely reacted with methanol. The number of moles of boron containing
product formed is
The molar conductivity of a solution of a weak acid HX (0.01 M) is 10 times smaller than the molar
conductivity of a solution of a weak acid HY (0.10 M). If 
the difference in their pKa values,
pKa (HX) - pKa (HY), is (consider degree of ionization of both acids to be << 1)
closed vessel with rigid walls contains 1 mol of 
and 1 mol of air at 298 K. Considering complete
decay of 
, the ratio of the final pressure to the initial pressure of the system at 298 K is
particles are ejected.SECTION 2
Q. No. 29-36 carry 4 marks each and 2 marks is deducted for every wrong answer.
Each question has FOUR options (A), (B), (C) and (D). ONE OR MORE THAN ONE of these four
option(s) is(are) correct
Q.
One mole of a monoatomic real gas satisfies the equation p(V – b) = RT where b is a constant. The
relationship of interatomic potential V(r) and interatomic distance r for the gas is given by
In the following reactions, the product S is
|
3 videos|3 docs|40 tests
|
|
3 videos|3 docs|40 tests
|
Top Courses for JEE
Important Questions for JEE Advanced 2015 Paper -2 with Solutions
JEE Advanced 2015 Paper -2 with Solutions MCQs with Answers
Online Tests for JEE Advanced 2015 Paper -2 with Solutions National Level Test Series for JEE Advanced 2025
|
© EduRev
|
Education Revolution
|
|
