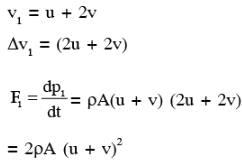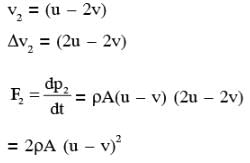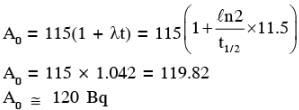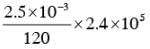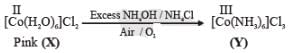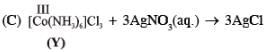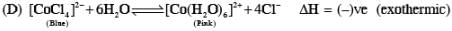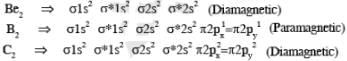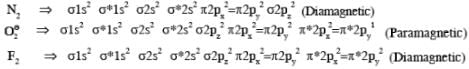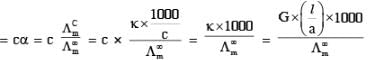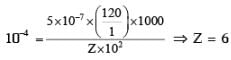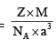JEE Advanced 2017 Paper - 1 with Solutions - JEE MCQ
30 Questions MCQ Test - JEE Advanced 2017 Paper - 1 with Solutions
A block M hangs vertically at the bottom end of a uniform rope of constant mass per unit length. The top end of the rope is attached to a fixed rigid support at O. A transverse wave pulse (Pulse 1) of wavelength λ0 is produced at point O on the rope. The pulse takes time TOA to reach point A. If the wave pulse of wavelength λ0 is produced at point A (Pulse 2) without disturbing the position of M it takes time TAO to reach point O. Which of the following options is/are correct ?.

A human body has a surface area of approximately 1 m2. The normal body temperature is 10 K above the surrounding room temperature T0. Take the room temperature to be T0 = 300 K. For T0 = 300 K, the value of 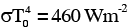 (where σ is the Stefan-Boltzmann constant). Which of the following options is/are correct ?
(where σ is the Stefan-Boltzmann constant). Which of the following options is/are correct ?
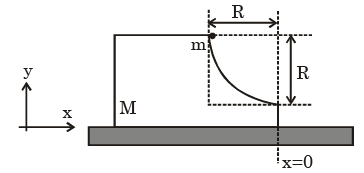
A block of mass M has a circular cut with a frictionless surface as shown. The block rests on the horizontal frictionless surface of a fixed table. Initially the right edge of the block is at x = 0, in a co-ordinate system fixed to the table. A point mass m is released from rest at the topmost point of the path as shown and it slides down. When the mass loses contact with the block, its position is x and the velocity is v. At that instant, which of the following options is/are correct ?
A circular insulated copper wire loop is twisted to form two loops of area A and 2A as shown in the figure. At the point of crossing the wires remain electrically insulated from each other. The entire loop lies in the plane (of the paper). A uniform magnetic field points into the plane of the paper.
At t = 0, the loop starts rotating about the common diameter as axis with a constant angular velocity ω in the magnetic field. Which of the following options is/are correct?
For an isosceles prism of angle A and refractive index µ, it is found that the angle of minimum deviation . Which of the following options is/are correct ?
In the circuit shown, L = 1 µH, C = 1 µF and R = 1 kΩ. They are connected in series with an a.c. source V = V0 sin ωt as shown. Which of the following options is/are correct ?
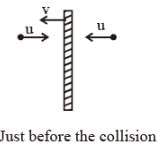
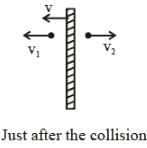
A flat plate is moving normal to its plane through a gas under the action of a constant force F. The gas is kept at a very low pressure. The speed of the plate v is much less than the average speed u of the gas molecules. Which of the following options is/are true ?
A drop of liquid of radius R = 10–2 m having surface tension divides itself into K identical drops. In this process the total change in the surface energy
then the value of α is
131I is an isotope of Iodine that β decays to an isotope of Xenon with a half-life of 8 days. A small amount of a serum labelled with 131I is injected into the blood of a person. The activity of the amount of 131I injected was 2.4 × 105 Becquerel (Bq). It is known that the injected serum will get distributed uniformly in the blood stream in less than half an hour. After 11.5 hours, 2.5 ml of blood is drawn from the person's body, and gives an activity of 115 Bq. The total volume of blood in the person's body, in liters is approximately
An electron in a hydrogen atom undergoes a transition from an orbit with quantum number ni to another with quantum number nf. Vi and Vf are respectively the initial and final potential energies of the electron. then the smallest possible nf is.
A monochromatic light is travelling in a medium of refractive index n = 1.6. It enters a stack of glass layers from the bottom side at an angle θ = 30°. The interfaces of the glass layers are parallel to each other.
The refractive indices of different glass layers are monotonically decreasing as nm = n – mΔn, where nm is the refractive index of the mth slab and Δn = 0.1 (see the figure). The ray is refracted out parallel to the interface between the (m - 1)th and mth slabs from the right side of the stack. What is the value of m ?
A stationary source emits sound of frequency f0 = 492 Hz. The sound is reflected by a large car approaching the source with a speed of 2 ms–1. The reflected signal is received by the source and superposed with the original. What will be the beat frequency of the resulting signal in Hz ? (Given that the speed of sound in air is 330 ms–1 and the car reflects the sound at the frequency it has received).
(Direction) Q.13, Q.14 and Q.15 by appropriately matching the information given in the three columns of the following table.
A charged particle (electron or proton) is introduced at the origin (x = 0, y = 0, z = 0) with a given initial velocity . A uniform electric field
and a uniform magnetic field
exist everywhere. The velocity
, electric field
and magnetic field
are given in column 1, 2 and 3, respectively. The quantities E0, B0 are positive in magnitude.
Column-1 Column-2 Column-3
Q. In which case will the particle move in a straight line with constant velocity ?
A charged particle (electron or proton) is introduced at the origin (x = 0, y = 0, z = 0) with a given initial velocity . A uniform electric field
and a uniform magnetic field
exist everywhere. The velocity
, electric field
and magnetic field
are given in column 1, 2 and 3, respectively. The quantities E0, B0 are positive in magnitude.
Column-1 Column-2 Column-3
Q. In which case will the particle describe a helical path with axis along the positive z-direction ?
A charged particle (electron or proton) is introduced at the origin (x = 0, y = 0, z = 0) with a given initial velocity . A uniform electric field
and a uniform magnetic field
exist everywhere. The velocity
, electric field
and magnetic field
are given in column 1, 2 and 3, respectively. The quantities E0, B0 are positive in magnitude.
Column-1 Column-2 Column-3
Q. In which case would the particle move in a straight line along the negative direction of y-axis (i.e., move along - ) ?
(Direction) Q.16, Q.17 and Q.18 by appropriately matching the information given in the three columns of the following table.
An ideal gas is undergoing a cyclic thermodynamics process in different ways as shown in the corresponding P–V diagrams in column 3 of the table. Consider only the path from state 1 to state 2. W denotes the corresponding work done on the system. The equations and plots in the table have standard notations as used in thermodynamics processes. Here g is the ratio of heat capacities at constant pressure and constant volume. The number of moles in the gas is n.
Q. Which of the following options is the only correct representation of a process in which ΔU = ΔQ - PΔV?
An ideal gas is undergoing a cyclic thermodynamics process in different ways as shown in the corresponding P–V diagrams in column 3 of the table. Consider only the path from state 1 to state 2. W denotes the corresponding work done on the system. The equations and plots in the table have standard notations as used in thermodynamics processes. Here g is the ratio of heat capacities at constant pressure and constant volume. The number of moles in the gas is n.
Q. Which one of the following options is the correct combination ?
An ideal gas is undergoing a cyclic thermodynamics process in different ways as shown in the corresponding P–V diagrams in column 3 of the table. Consider only the path from state 1 to state 2. W denotes the corresponding work done on the system. The equations and plots in the table have standard notations as used in thermodynamics processes. Here g is the ratio of heat capacities at constant pressure and constant volume. The number of moles in the gas is n.
Q. Which one of the following options correctly represents a thermodynamics process that is used as a correction in the determination of the speed of sound in an ideals gas ?
The IUPAC name(s) of the following compound is (are)
The correct statement(s) for the following addition reactions is(are)
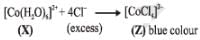
Addition of excess aqueous ammonia to a pink coloured aqueous solution of MCl2 . 6H2O (X) and NH4Cl gives an octahedral complex Y in the presence of air. In aqueous solution, complex Y behaves as 1 : 3 electrolyte. The reaction of X with excess HCl at room temperature results in the formation of a blue coloured complex Z. The calculated spin only magnetic moment of X and Z is 3.87 B.M., whereas it is zero for complex Y.
Q. Among the following options, which statment is (are) ?
For a solution formed by mixing liquids L and M, the vapour pressure of L plotted against the mole fraction of M in solution is shown in the following figure, Here xL and xM represent mole fractions of L and M, respectively, in the solution. the correct statement(s) applicable to this system is(are) -
An ideal gas is expanded from (p1 , V1 , T1) to (p2 , V2 , T2) under different conditions. The correct statement(s) among the following is(are)
The correct statements(s) about the oxoacids, HClO4 and HClO, is (are) -
The colour of the X2 molecules of group 17 elements changes gradually from yellow to violet down the group. This is due to -
Among H2, He+2, Li2, Be2, B2, C2, N2, O-2, the number of diamagnetic species is -( Atomic number) : H =1, He = 2, Li = 3, Be = 4, B = 5, C = 6, N = 7,I = 8, F = 9)
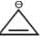
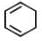
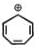
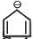
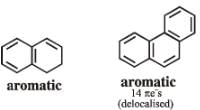
Among the following, the number of aromatic compound (s) is-
The conductance of a 0.0015 M aqueous solution of a weak monobasic acid was determined by using a conductivity cell consisting of platinized Pt electrodes. The distance between the electrodes is 120 cm with an area of cross section of 1 cm2. The conductance of this solution was found to be 5 × 10–7S. The pH of the solution is 4. The value of limiting molar conductivity of this weak monobasic acid in aquence solution is
The metal used to recover copper from a solution of copper sulphate is
A crystalline solid of a pure substance has a face-centred cubic structure with a cell edge of 400 pm. If the density of the substance in the crystal is 8g cm–3, then the number of atoms present in 256g of the crystal is N × 1024. The value of N is


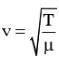 and it is property of medium.
and it is property of medium.