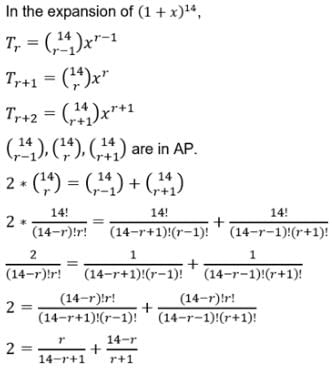JEE Advanced Level Test: Binomial Numbers- 2 - JEE MCQ
25 Questions MCQ Test - JEE Advanced Level Test: Binomial Numbers- 2
Let n be a positive integer. Then of the following, the greatest term is
The sum of the series (12 + 1) 1! + (22 + 1).2! + (32 + 1).3! ...+(n2 + 1). n! is
The last two digits of the number 3400 are
The sum of the co-efficients of all the even powers of x in the expansion of (2x2 – 3x + 1)11 is
The coefficient of xr(0 < r < n – 1) in the expression (x + 2)n-1 + (x + 2)n-2 . (x + 1) + (x + 2)n-3. (x + 1)2 + .............+ (x + 1)n- is
The co-efficient of x401 in the expansion of (1 + x + x2 + ........+x9)-1, (|x| < 1) is
Let (1 + x2)2 (1 + x)n = A0 + A1x + A2x2 + ........... If A0, A1, A2 are in A.P. then the value of n is
The number 101100 – 1 is divisible by
If the 6th term in the expansion of when x = 3 is numerically greatest then the possible integral value(s) of n can be
If where I, n are integers and 0 < f < 1, then
Positive integers can be represented as
The co-efficient of the middle term in the expansion of (1 + x)2n is
The value of nC0 . nCn + nC1 . nCn – 1 + ... + nCn . nC0 is
The value of r for which 30Cr . 20C0 + 30Cr – 1 . 20C1 +...+ 30C0 . 20C r is maximum, is
The value of r(0 < r < 30) for which 20Cr . 10C0 + 20Cr – 1 . 10C1 +...+ 20C0 . 10Cr is minimum, is
The value of r(0 < r < 30) for which 20Cr . 10C0 + 20Cr – 1 . 10C1 +...+ 20C0 . 10Cr is minimum, is
Column-I Column-II
(A) If l be the number of terms in the expansion of (P) O + T = 3
(1 + 5x + 10x2 + 10x2 + 5x4 + x5)20 and if unit's
place and ten's place digits in 3l are O and T, then
(B) If l be the number of terms in the expansion (Q) O + T = 7
of and if unit's place and (R) O + T = 9
ten's place digits in 7l are O and T, then
(C) If l be the number of terms in the
expansion of (1 + x)101 (1 + x2 _ x)100 (S) T _ O = 7
and if unit's place and ten's place
digits in 9l are O and T, then (T) O _ T = 7
subjective type
Find the coefficients
(i) x7 in (ii) x _7 in
(iii) Find the relation between a and b, so that these coefficients are equal.
If the coefficients of (2r + 4)th , (r – 2)th terms in the expansion of (1 + x)18 are equal, find r.
If the coefficients of the rth, (r + 1)th and (r + 2)th terms in the expansion of (1 + x)14 are in A.P., find r.
Find the term independent of x in the expansion of
(a) (b)
Given that (1 + x + x2)n = a0 + a1x + a2x2 + ...... +a2nx2n, find the values of
(i) a0 + a1 + a2 + ..... + a2n ;
(ii) a0 _ a1 + a2 _ a3 ....... +a2n ;
(iii) a02 _ a12 + a22 _ a32 + ... + a2n2
In a Binomial Distribution, if ‘n’ is the number of trials and ‘p’ is the probability of success, then the mean value is given by
Prove that :
n _ 1Cr + n _ 2Cr + n _ 3Cr + ............ + rCr = nCr + 1.