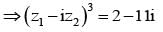JEE Advanced Level Test: Complex Number- 4 - JEE MCQ
30 Questions MCQ Test - JEE Advanced Level Test: Complex Number- 4
Let z(α,β) = cosα + eiβ sinα (α, β ∈ R, i = √-1) then the exhaustive set of values of modulus of z(θ, 2θ), as θ varies, is
If z = x + iy be a non real complex number and a1 , a2 , a3 , b1 , b2 , b3 are all real,then


If then the maximum value of |Z| is equal to
Let Z1 = 10+ 6i and Z2 = 4+6i . If Z be a complex number such that Then |Z - 7 -9i| =
If a complex number Z satisfy, |2Z + 10 + 10i | < 5√3 - 5 then the least principal argument of Z is
If a,b,c are integers not all equal andw is a cube root of unity (ω ≠ 1) then the minimum value of |a + bω+ cω2| is
If 1, w, w2 .....wn-1 are nth roots of 1 then value of equals to
If 1, α1, α2 ,.......α99 are roots of Z100 = 1 then 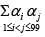 equal to
equal to
If cosx + 2cosy + 3cosz = sin x + 2siny + 3sinz = 0 then the value of sin 3x + 8sin 3y+ 27 sin 3z is
Let a complex number z, with minimum argument is lying on the cure |z + 4i| = 2 then
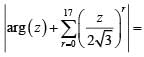
Number of ordered pairs (a,b) of real numbers such that (a + ib)2012 = a - ib holds good is
If | z - 3i| = 3, (where i = √-1) and arg z ∈ (0, π/2), then cot (arg (z)) 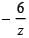 is equal to
is equal to
If α0, α1, α2, ...αn-1 be the nth roots of unity, then value of is equal to
The least value of P for which the two curves arg z = π/6 and |z - 2 √3i| = P have a solution is ..
If |z -i| ≤ 2 and z0 = 5+3i , the maximum value of |iz + z0| is
For all complex numbers z1 ,z2 satisfying |z1| = 12 and |z2 - 3 - 4i| = 5 , the minimum value of |z1 -z2| is
If b ≠ 1 be any nth root of unity then 1 + 3β + 5β2 + ........n terms equals
The number of solutions of the equation is
If a1, a2,--------an are real numbers and cos α + isin α is a root of zn +a1zn-1 + a2zn-2 +-----+an-1z+an = 0, then the value of a1 cos α + a2 cos 2α + a3 cos 3α + ------ +an cos na is
If |z – 1| + |z + 3| ≤ 8, then the range of values of |z – 4| is,
If a, b, c, a1 , b1 , c1 are non zero complex numbers satisfying and
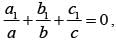
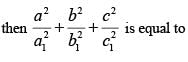
Let z and w be complex numbers such that and arg zω =π, then arg z =
Let z = cosθ + isinθ. Then the value of 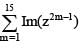 at θ = 2° is
at θ = 2° is
let a be a complex number such that |a| = 1 If the equation az2 + z + 1 =0 has a pure imaginary root, then tan (arg a) =
is purely imaginary, then number of values of a in [0, 2π ] is---
If z1z2 ∈ C, 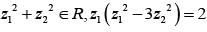 and
and 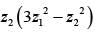 = 11 then the value of
= 11 then the value of 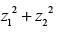 is
is


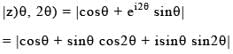
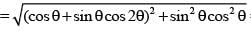
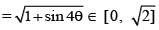
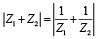 then (Z1, Z2 ∈C)
then (Z1, Z2 ∈C)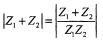
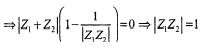


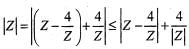
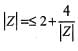
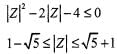
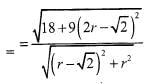
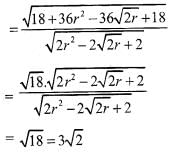
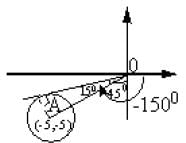

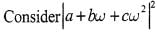
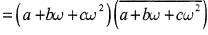
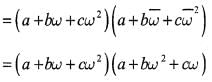
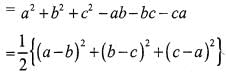
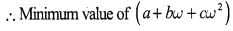
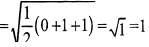





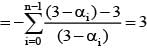
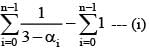
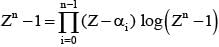
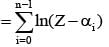
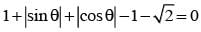
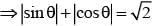
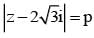 represents a circle of radius p having centre at (0, 2 √3) and arg z = π/6 is a line making an angle of 300 with OX and lying in 1st quadrant.
represents a circle of radius p having centre at (0, 2 √3) and arg z = π/6 is a line making an angle of 300 with OX and lying in 1st quadrant. 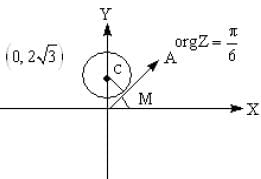
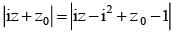
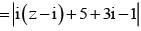
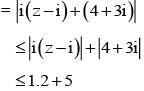
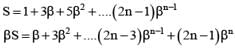
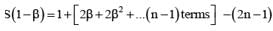
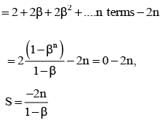
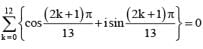
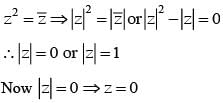

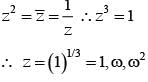
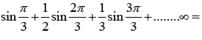
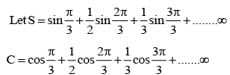
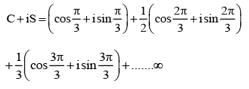
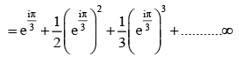
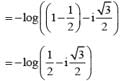
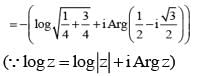
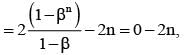
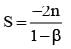
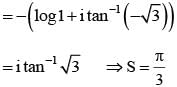
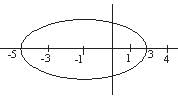
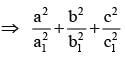
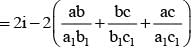
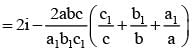

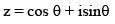
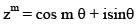
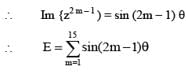
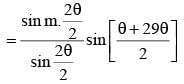
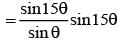
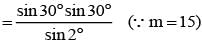
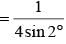
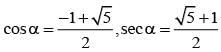
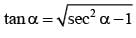
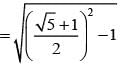
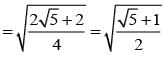
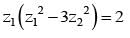 ............. (i)
............. (i)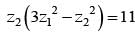 ............. (ii)
............. (ii)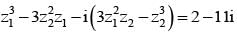 ............. (iv)
............. (iv)