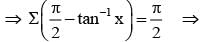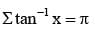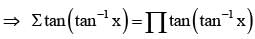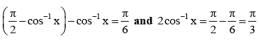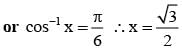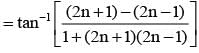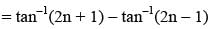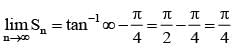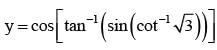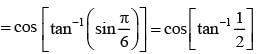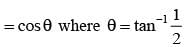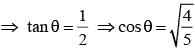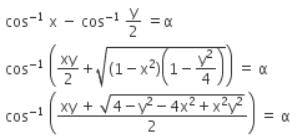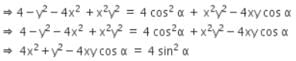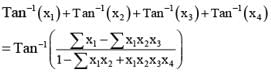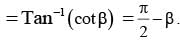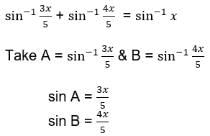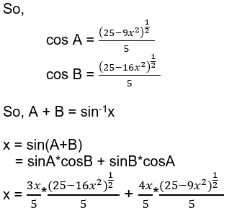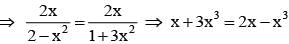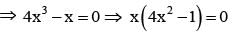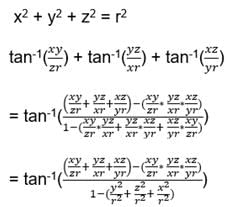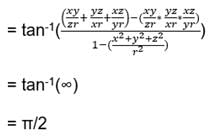JEE Advanced Level Test: Inverse Trigonometry- 1 - JEE MCQ
30 Questions MCQ Test Chapter-wise Tests for JEE Main & Advanced - JEE Advanced Level Test: Inverse Trigonometry- 1
If cot-1 x + cot-1 y + cot-1 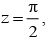 then x + y + z is equal to
then x + y + z is equal to
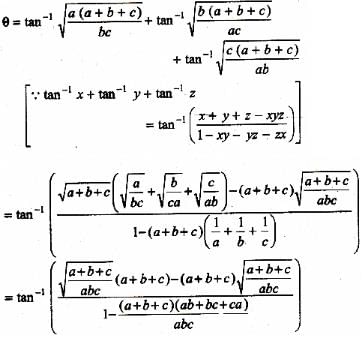
If a, b, c be positive real numbers and the value of 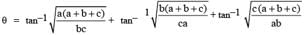 then tanθ is equal to -
then tanθ is equal to -
The value of tan–1(1) + cos–1(–1/2) + sin–1(–1/2) is equal to -
The Greatest value among tan1, tan-11, sin1, sin-11, cos1
Where a and b are in their lowest form, then (a + b) equal to
If domain of function f:x→x² + 1 is {0,1}, then its range is
The sum of the series cot–12 + cot–18 + cot–118 + cot–132 + ….. is
If tan (x + y) = 33 and x = tan–1 3, then y will be
The number of solutions of the equation belonging to the interval ( 0,1) is
If cos-1 x - cos-1 y/2 = α, then 4x2 − 4xy cos α + y2 is equal to
If [sin-1 cos-1 sin-1 tan-1x] = 1, ëû where [.] denotes the greatest integer function, then x belongs to the interval.
The value of sin-1 [cos(cos-1(cosx) + sin-1 (sinx))], where
If x1, x2 , x3 , x4 are roots of the equation x4 - x3 sin 2β + x2 cos2β - x cosβ - sinβ Tan-1 (x1) + Tan-1 (x2) + Tan-1 (x3) + Tan-1(x4) can be equal to
If xy + yz + zx = 1, then, tan–1x + tan–1y + tan–1z =
then the value of tan-1 (sin A) + tan-1(sin3 A) + tan-1 (cot A cos A)
If 0 < x < 1, the numberof solutions of the equation tan-1(x-1) + tan-1 x + tan-1 (x+1) = tan-1 3x is
|
446 docs|930 tests
|