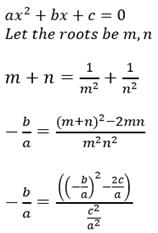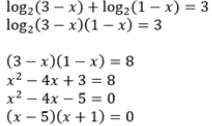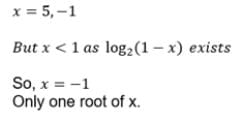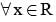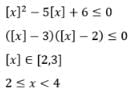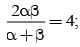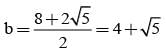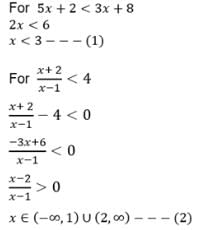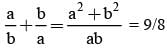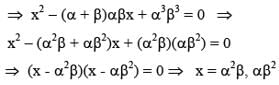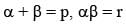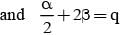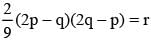JEE Advanced Level Test: Quadratic Equation- 1 - JEE MCQ
30 Questions MCQ Test Chapter-wise Tests for JEE Main & Advanced - JEE Advanced Level Test: Quadratic Equation- 1
If the sum of the roots of the equation ax2 + bx + c = 0 is equal to sum of the squares of their reciprocals, then bc2 , ca2 , ab2 are in
If k > 0 and the product of the roots of the equation x2 - 3kx + 2e2logk -1 = 0 is 7 then the sum of the roots is
The number of real solution of the equation (9/10)x = -3 + x - x2 is
If the roots of (x - a)(x - b) +(x - b)(x - c) + (x - c)(x - a) = 0 are equal then which of the following is not possible
The equation log2 (3- x) + log2 (1- x) = 3 has
If ax2 + bx + c = 0 and bx2 + cx + a = 0 have a common a ≠ 0
If a, b are the roots of x2 + px + 1 = 0, and c, d are the roots of x2 + qx + 1 = 0, then the value of E = (a - c)(b - c)(a+ d)(b+ d) is
If x2 + 2ax +10 - 3a > 0 for each x ∈ R, then
If a, b, c are real and a ≠ b, then the roots of the equation 2(a - b)x2 -11(a + b + c)x - 3(a - b) = 0 are
The set of values of x for which the inequality [x]2 - 5[x] + 6 < 0 (where [.] denote the greatest integral function) hold good is
If the sum of n terms of an A.P. is 2n2 + 5n, then find the 4th term.
If the harmonic mean between the roots of (5 + √2)x2 - bx + (8 + 2√5) = 0 is 4, then the value of b is
If α, β are the roots of x2 + ax - b = 0 and γ,δ are the roots of x2 + ax + b = 0 then (α - γ) (α - δ) (β - δ) (β - γ) =
If the ratio of the roots of ax2 + 2bx + c = 0 is same as the ratio of the roots of px2 + 2qx + r = 0 then
The roots of the equation (b - c) x2 + 2 (c - a)x +(a - b) = 0 are always
If a ∈ Z and the equation (x - a)(x -10) +1 = 0 has integral roots, then values of ‘a’ are
The value of λ in order that the equations 2x2 + 5λx + 2 = 0 and 4x2 + 8λx + 3 = 0 have a common root is given by
If both roots of the equation x2 - 2ax + a2 -1 = 0 lie in the interval (-3,4) then sum of the integral parts of ‘a’ is
Number of rational roots of the equation |x2 - 2x - 3| + 4x = 0 is
The set of real values of x satisfying |x-1| < 3 and |x - 1| > 1
Let f(x) be a polynomial for which the remainders when divided by x – 1, x – 2, x – 3 respectively 3, 7, 13. Then the remainder of f(x) when divided by (x – 1) (x – 2) (x – 3) is
The range of values of x which satisfy 5x + 2 < 3x + 8 and 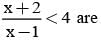
Suppose a2 = 5a – 8 and b2 = 5b – 8, then equation whose roots are a/b and b/a is
If α,β are roots of ax2 + bx + c = 0, then roots of a3x2 + abcx + c3 = 0 are
If P(x) = ax2 + bx + c and Q(x) = -ax2 + dx + c, where ac ≠ 0, then P(x)Q(x) = 0 has
If the product of the roots of the equation x2 – 5kx + 2e4 ln k - 1 = 0 is 31, then sum of the root is
Let α, β be the roots of the equation x2 - px + r = 0 and (α/2), 2β be the roots of the equation x2 - qx + r = 0. Then the value of r is
The sum of all the real roots of the equation |x – 2|2 + |x – 2| – 2 = 0 is
|
481 docs|964 tests
|