JEE Advanced Level Test: Vector Algebra- 1 - JEE MCQ
30 Questions MCQ Test - JEE Advanced Level Test: Vector Algebra- 1
The differential equation of all parabola each of which has a latus rectum 4a and whose axis parallel to the x-axis is
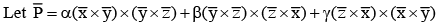 and
and 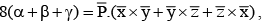 for positive numbers α, β and γ, then value of
for positive numbers α, β and γ, then value of 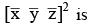
are any two vectors of magnitudes 1 and 2 respectively, and
then the angle between
Volume of parallelopiped determined by vectors Then the volume of the parallelopiped determined by vectors
4-points whose position vector are coplanar and
then the least value of
are unit vectors, satisfying
then value of
If are mutually perpendicular vectors and
are perpendicular to
respectively and if
are three unit non-coplanar vectors such that
is a vector such that
In be the position vectors of X, Y and Z with respect of the origin O, respectively. If the distance of Z from the bisector of the acute angle of
then sum of all possible values of β is
Least value of the volume of the parallelopiped formed by the vectors
Equation of the plane containing the straight line and perpendicular to the plane containing the straight lines
If the distance of the point P (1, –2, 1) from the plane x + 2y – 2z = α , where α > 0, is 5, then the foot of the perpendicular from P to the plane is
The equation of a plane passing through the line of intersection of the planes x + 2y + 3z = 2 and x - y + z = 3 and at a distance from the point (3, 1, –1) is
Two lines are coplanar. Then α can not take value
A line with direction cosines proportional to 2, 1, 2 meets each of the lines x = y + a = z and x + a = 2y = 2z. The co-ordinates of each of the points of intersection are given by
be three non-coplanar unit vectors such that the angle between every pair of them is
where p, q and r are scalars, then the value of
The image of line in the plane 2x - y + z + 3 = 0 in the line
The distance of the point (1,–5,9) form the plane x - y + z = 5 measured along a straight line x = y = z is
Perpendiculars are drawn from points on the line to the plane x + y + z = 3. The feet of perpendiculars lie on the line
A variable plane at a distance of 1 unit from the origin cut the co-ordinate axis at A, B and C. If the centroid D (x, y, z) of DABC satisfy the relation then value of k is
A variable plane is at a constant distance 3p form the origin and meets the axes in A, B and C. The locus of the centroid of the triangle ABC is
If the lines are coplanar, then k can have
If the angle θ between the line and plane
such that
Then, value of λ is
The point of intersection of the lines must be














