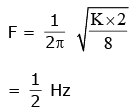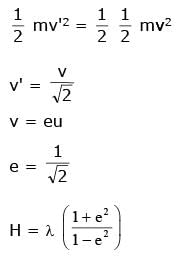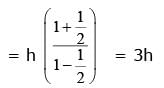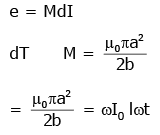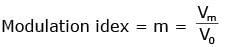JEE Main 2017 April 8 Paper & Solutions - JEE

An object is dropped from a height h from the ground. Every time it hits the ground it looses 50% of its kinetic energy. The total distance covered as t→∞ is :

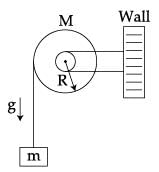
A uniform disc of radius R and mass M is free to rotate only about its axis. A string is wrapped over its rim and a body of mass m is tied to the free end of the string as shown in the figure. The body is released from rest. Then the acceleration of the body is :

Moment of inertia of an equilateral triangular lamina ABC, about the axis passing through its centre O and perpendicular to its plane is I_o as shown in the figure.  A cavity DEF is cut out from the lamina, where D, E, F are the midpoints of the sides. Moment of inertia of the remaining part of lamina about the same axis is :

If the Earth has no rotational motion, the weight of a person on the equator is W. Determine the speed with which the earth would have to rotate about its axis so that the person at the equator will weigh 3/4 W. Radius of the Earth is 6400 km and g=10 m/s².

In an experiment, a sphere of aluminium of mass 0.20 kg is heated up to 150ºC. Immediately, it is put into water of volume 150 cc at 27ºC kept in a calorimeter of water equivalent to 0.025 kg.  Final temperature of the system is 40ºC. The specific heat of aluminium is :
(take 4.2 Joule=1 calorie)

A compressive force, F is applied at the two ends of a long thin steel rod. It is heated, simultaneously, such that its temperature increases by ∆T.  The net change in its length is zero.  Let l be the length of the rod, A it's area of cross-section, Y its Young’s modulus, and α it's coefficient of linear expansion. Then, F is equal to :

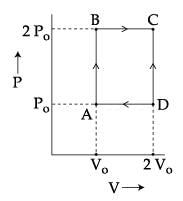
An engine operates by taking n moles of an ideal gas through the cycle ABCDA shown in figure. The thermal efficiency of the engine is :
(Take C_v=1.5 R, where R is gas constant)

An ideal gas has molecules with 5 degrees of freedom. The ratio of specific heats at constant pressure (C_p) and at constant volume (C_v) is:

The ratio of maximum acceleration to maximum velocity in a simple harmonic motion is 10 s⁻¹. At, t=0 the displacement is 5 m. What is the maximum acceleration? The initial phase is π/4.

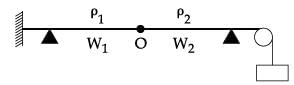
Two wires W₁ and W₂ have the same radius r and respective densities ρ₁ and ρ₂ such that ρ₂=4ρ₁. They are joined together at the point O, as shown in the figure. The combination is used as a sonometer wire and kept under tension T.The point O is midway between the two bridges. When a stationary wave is set up in the composite wire, the joint is found to be a node. The ratio of the number of antinodes formed in W₁ to W₂ is :

There is a uniform electrostatic field in a region. The potential at various points on a small sphere centred at P, in the region, is found to vary between the limits 589.0 V to 589.8 V. What is the potential at a point on the sphere whose radius vector makes an angle of 60º with the direction of the field?

The energy stored in the electric field produced by a metal sphere is 4.5 J. If the sphere contains 4 µC charges, its radius will be: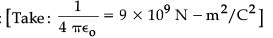 

What is the conductivity of a semiconductor sample having electron concentration of 5×10¹⁸ m⁻³, hole concentration of 5×10¹⁹ m⁻³, electron mobility of 2.0 m² V⁻¹  s⁻¹ and hole mobility of 0.01 m² V⁻¹ s⁻¹?
(Take charge of electron as 1.6×10⁻¹⁹ C)

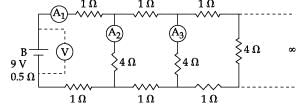
A 9 V battery with internal resistance of 0.5 Ω is connected across an infinite network as shown in the figure. All ammeters A₁, A₂, A₃ and voltmeter V are ideal.

In a certain region static electric and magnetic fields exist. The magnetic field is given by 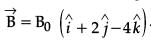 .  If a test charge moving with a velocity 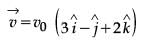experiences no force in that region, then the electric field in the region, in SI units, is :

A magnetic dipole in a constant magnetic field has:

A small circular loop of wire of radius a is located at the centre of a much larger circular wire loop of radius b. The two loops are on the same plane. The outer loop of radius b carries an alternating current I=I_o cos (ωt). The emf induced in the smaller inner loop is nearly :

Magnetic field in a plane electromagnetic wave is given by

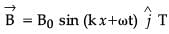
Expression for corresponding electric field will be :
Where c is speed of light.

Let the refractive index of a denser medium with respect to a rarer medium be n₁₂ and its critical angle is θ_C. At an angle of incidence A when light is travelling from denser medium to rarer medium, a part of the light is reflected and the rest is refracted and the angle between reflected and refracted rays is 90⁰. Angle A is given by :

A single slit of width b is illuminated by a coherent monochromatic light of wavelength λ. If the second and fourth minima in the diffraction pattern at a distance 1 m from the slit are at 3 cm and 6 cm respectively from the central maximum, what is the width of the central maximum? (i.e. distance between first minimum on either side of the central maximum)

The maximum velocity of the photoelectrons emitted from the surface is v when light of frequency n falls on a metal surface. If the incident frequency is increased to 3n, the maximum velocity of the ejected photoelectrons will be :

According to Bohr’s theory, the time averaged magnetic field at the centre (i.e. nucleus) of a hydrogen atom due to the motion of electrons in the n^th orbit is proportional to : (n=principal quantum number)

Two deuterons undergo nuclear fusion to form a Helium nucleus. Energy released in this process is : (given binding energy per nucleon for deuteron=1.1 MeV and for helium=7.0 MeV)

The V-I characteristic of a diode is shown in the figure. The ratio of forward to reverse bias resistance is :

A signal of frequency 20 kHz and peak voltage of 5 Volt is used to modulate a carrier wave of frequency 1.2 MHz and peak voltage 25 Volts. Choose the correct statement.

In a physical balance working on the principle of moments, when 5 mg weight is placed on the left pan, the beam becomes horizontal. Both the empty pans of the balance are of equal mass. Which of the following statements is correct?

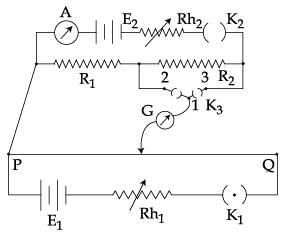
A potentiometer PQ is set up to compare two resistances as shown in the figure. The ammeter A in the circuit reads 1.0 A when two way key K₃ is open. The balance point is at a length l₁ cm from P when two way key K₃ is plugged in between 2 and 1, while the balance point is at a length l₂ cm from P when key K₃ is plugged in between 3 and 1. The ratio of two resistances R₁/R₂ , is found to be :

Among the following, correct statement is :

Excess of NaOH (aq) was added to 100 mL of FeCl₃ (aq) resulting into 2.14 g of Fe(OH)₃. The molarity of FeCl₃ (aq) is
(Given molar mass of Fe=56 g mol⁻¹ and molar mass of Cl=35.5 g mol⁻¹)

Among the following, the incorrect statement is :

For a reaction, A(g) → A(l); ∆H=−3RT. The correct statement for the reaction is :

What is the standard reduction potential (E^o) for Fe³⁺ → Fe ?
Given that :
Fe²⁺ +2^e- → Fe; E^o _Fe²⁺_/Fe = -0.47V
Fe³⁺ + e^- → Fe²⁺ ; E^o _Fe³⁺_/Fe²⁺ = +0.77V

If the shortest wavelength in Lyman series of hydrogen atom is A, then the longest wavelength in Paschen series of He⁺ is:

5 g of Na₂SO₄ was dissolved in x g of H₂O. The change in freezing point was found to be 3.82^oC. If Na₂SO₄ is 81.5% ionised, the value of x
(K_f for water=1.86^oC kg mol⁻¹) is approximate:
(molar mass of S=32 g mol⁻¹ and that of Na=23 g mol⁻¹)

Addition of sodium hydroxide solution to a weak acid (HA) results in a buffer of pH 6. If ionisation constant of HA is 10⁻⁵, the ratio of salt to acid concentration in the buffer solution will be:

The rate of a reaction A doubles on increasing the temperature from 300 to 310 K. By how much, the temperature of reaction B should be increased from 300 K so that rate doubles if activation energy of the reaction B is twice to that of reaction A.

The enthalpy change on freezing of 1 mol of water at 5^oC to ice at −5^oC is :
(Given ∆_fusH=6 kJ mol⁻¹ at 0^oC, C_p(H₂O, l)=75.3 J mol⁻¹ K⁻¹, C_p(H₂O, s)=36.8 J mol⁻¹ K⁻¹)

Which of the following is paramagnetic?

The pair of compounds having metals in their highest oxidation state is:

sp³d² hybridization is not displayed by :

Identify the pollutant gases largely responsible for the discoloured and lustreless nature of marble of the Taj Mahal.

In which of the following reactions, hydrogen peroxide acts as an oxidizing agent?

Consider the following ionization enthalpies of two elements ‘A’ and ‘B’.

Consider the following standard electrode potentials (E^o in volts) in aqueous solution:

Based on these data, which of the following statements is correct?

A metal ‘M’ reacts with nitrogen gas to afford ‘M₃N’. ‘M₃N’ on heating at high temperature gives back ‘M’ and on reaction with water produces a gas ‘B’. Gas ‘B’ reacts with aqueous solution of CuSO₄ to form a deep blue compound. ‘M’ and ‘B’ respectively are :

The number of S=O and S−OH bonds present in peroxodisulphuric acid and pyrosulphuric acid respectively are:

A solution containing a group-IV cation gives a precipitate on passing H₂S. A solution of this precipitate in dil.HCl produces a white precipitate with NaOH solution and bluish-white precipitate with basic potassium ferrocyanide. The cation is :

A mixture containing the following four compounds is extracted with 1M HCl. The compound that goes to aqueous layer is:

The reason for “drug induced poisoning” is :

Which of the following compounds will not undergo Friedel Craft’s reaction with benzene?

Among the following, the essential amino acid is:

The major product expected from the following reaction is:

The major product of the following reaction is :

Which of the following statements is not true about partition chromatography?

The IUPAC name of the following compound is :

The major product of the following reaction is:

The major product of the following reaction is:

Let f(x)=2¹⁰⋅x+1 and g(x)=3¹⁰⋅x−1. If (fog)(x)=x, then x is equal to :

Let p(x) be a quadratic polynomial such that p(0)=1. If p(x) leaves remainder 4 when divided by x−1 and it leaves remainder 6 when divided by x+1; then :

Let z∈C, the set of complex numbers. Then the equation, 2|z+3i|−|z−i|=0 represents :

The number of real values of λ for which the system of linear equations
2x+4y−λz=0
4x+λy+2z=0
λx+2y+2z=0
has infinitely many solutions, is :

Let A be any 3×3 invertible matrix. Then which one of the following is not always true?

If all the words, with or without meaning, are written using the letters of the word QUEEN and are arranged as in English dictionary, then the position of the word QUEEN is :

If (27)⁹⁹⁹ is divided by 7, then the remainder is :

If the arithmetic mean of two numbers a and b, a > b > 0, is five times their geometric mean, then a+b / a-b is equal to:

If the sum of the first n terms of the series √3 + √75 + √243 + √507 + .... + 435√3 then n equals :

 is equal to:

The tangent at the point (2, −2) to the curve, x²y²−2x=4(1−y) does not pass through the point :

If then  is equal to :

If a point P has co-ordinates (0, −2) and Q is any point on the circle, x²+y²−5x−y+5=0, then the maximum value of (PQ)² is :

The integral  is equal to :
(where C is a constant of integration)

The integral equals :

The area (in sq. units) of the smaller portion enclosed between the curves, x²+y²=4 and y²=3x, is :

The curve satisfying the differential equation, ydx−(x+3y²)dy=0 and passing through the point (1, 1), also passes through the point :

The locus of the point of intersection of the straight lines,
tx−2y−3t=0
x−2ty+3=0  (t ∈ R), is :

If two parallel chords of a circle, having diameter 4 units, lie on the opposite sides of the centre and subtend angles cos ^-1 (1/7) and sec^-1 (7) at the centre respectively, then the distance between these chords, is :

If the common tangents to the parabola, x²=4y and the circle, x²+y²=4 intersect at the point P, then the distance of P from the origin, is :

Consider an ellipse, whose centre is at the origin and its major axis is along the x-axis. If its eccentricity is 3/5 and thedistance between its foci is 6, then the area (in sq. units) of the quadrilateral inscribed in the ellipse, with the vertices as the vertices of the ellipse, is :

The coordinates of the foot of the perpendicular from the point (1, −2, 1) on the plane containing the lines,  and  is :

The line of intersection of the planes  and  is :

The area (in sq. units) of the parallelogram whose diagonals are along the vectors  and  is:

The mean age of 25 teachers in a school is 40 years. A teacher retires at the age of 60 years and a new teacher is appointed in his place.  If now the mean age of the teachers in this school is 39 years, then the age (in years) of the newly appointed teacher is :

Three persons P, Q and R independently try to hit a target. If the probabilities of their hitting the target are 3/4, 1/2 and 5/8 respectively, then the probability that the target is hit by P or Q but not by R is :

An unbiased coin is tossed eight times. The probability of obtaining at least one head and at least one tail is:

If
then  is equal to : 

The value of   is equal to :

The proposition (~p) ∨ (p ∧ ~q) is equivalent to :