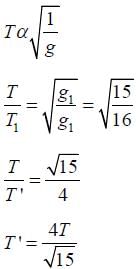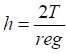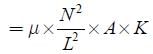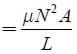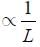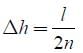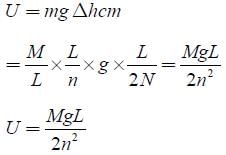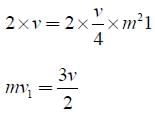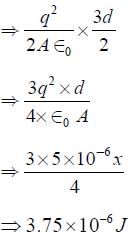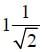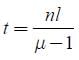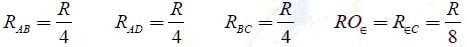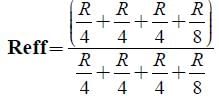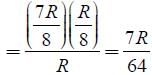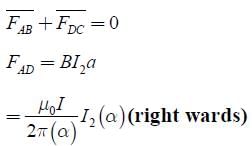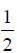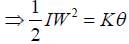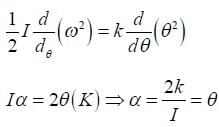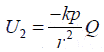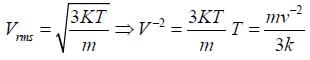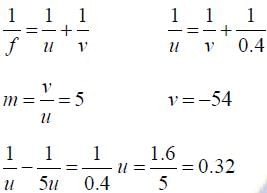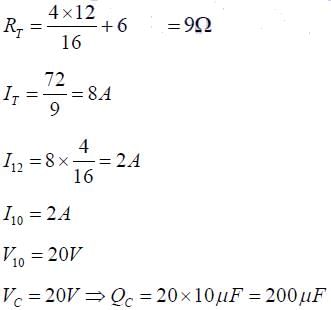JEE Main 2019 April 9 Shift 1 Paper & Solutions - JEE MCQ
30 Questions MCQ Test - JEE Main 2019 April 9 Shift 1 Paper & Solutions
The magnetic field of a plane electromagnetic wave is given by:
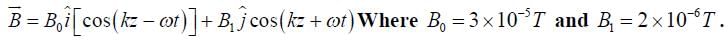
The rms value of the force experienced by a stationary charge Q =10–4C at z = 0 is
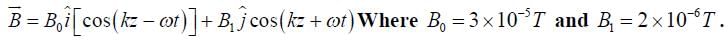
The rms value of the force experienced by a stationary charge Q =10–4C at z = 0 is
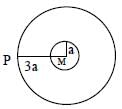
A solid sphere of mass ‘M’ and radius ‘a’ is surrounded by a uniform concentric spherical shell of thickness 2a and mass 2M. The gravitational field at distance ‘3a’ from the centre will be:
A moving coil galvanometer has resistance 50Ω and it indicates full deflection at 4mA current. A voltmeter is made using this galvanometer and a 5 kΩ resistance.The maximum voltage, that can be measured using this voltmeter, will be close to:
For a given gas at 1 atm pressure, rms speed of the molecules is 200 m/s at 127ºC. At 2 atm pressure and at 227ºC, the rms speed of the molecules will be:
Taking the wavelength of first Balmer line in hydrogen spectrum (n = 3 to n = 2) as 660 nm, the wavelength of the 2nd Balmer line (n = 4 to n = 2) will be:
The pressure wave, P = 0.01sin[1000t – 3x]Nm–2 , corresponds to the sound produced
by a vibrating blade on a day when atmospheric temperature is 0ºC. On some other day when temperature is T, the speed of sound produced by the same blade and at the same frequency is found to be 336ms–1 . Approximate value of T is:
The following bodies are made to roll up (without slipping) the same inclined plane from a horizontal plane :
(i) a ring of radius R,
(ii) a solid cylinder of radius R/2 and
(iii) a solid sphere of radius R/4. If, in each case, the speed of the center of mass at the bottom of the incline is same, theratio of the maximum heights they climb is:
An NPN transistor is used in common emitter configuration as an amplifier with1kΩ load resistance. Signal voltage of 10 mV is applied across the base-emitter. Thisproduces a 3 mA change in the collector current and 15μ A change in the basecurrent of the amplifier. The input resistance and voltage gain are:
A ball is thrown vertically up (taken as +z-axis) from the ground. The correct momentum – height (p-h) diagram is:
The electric field of light wave is given as 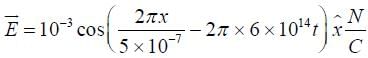 .
.
The light falls on a metal plate of work function 2eV. The stopping potential of the
photo-electrons is:Given, E (in eV) 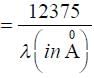
A string is clamped at both the ends and it is vibrating in its 4th harmonic. The equation of the stationary wave is Y= 0.3sin(0.157x)cos(200π) . The length of the string is: (All quantities are in SI units.)
A signal Acosωt is transmitted using ν0 sin ω0t as carrier wave. The correct amplitude modulated (AM) signal is:
In the density measurement of a cube, the mass and edge length are\ measured as (10.00 ± 0.10) kg and ( 0.10 ± 0.01) m, respectively. The error in the measurement of density is:
A simple pendulum oscillating in air has period T. The bob of the pendulum is
completely immersed in a non-viscous liquid. The density of the liquid is 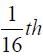 of the material of the bob. If the bob is inside liquid all the time, its period of oscillation in this liquid is:
of the material of the bob. If the bob is inside liquid all the time, its period of oscillation in this liquid is:
If ‘M’ is the mass of water that rises in a capillary tube of radius ‘r’, then mass of
water which will rise in a capillary tube of radius ‘2r’ is:
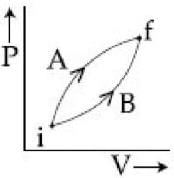
Following figure shows two process A and B for a gas. If ΔQA and ΔQB are the amount of heat absorbed by the system in two cases, and ΔUA and ΔUB are changes in internal energies, respectively, then:
The total number of turns and cross-section area in a solenoid is fixed. However, its length L is varied by adjusting the separation between windings. The inductance of solenoid will be proportional to:
A uniform cable of mass ‘M’ and length ‘L’ is placed on a horizontal surface such
that its 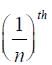 part is hanging below the edge of the surface. To lift the hanging part of the cable upto the surface, the work done should be:
part is hanging below the edge of the surface. To lift the hanging part of the cable upto the surface, the work done should be:
A body of mass 2 kg makes an elastic collision with a second body at rest andcontinues to move in the original direction but with one fourth of its original speed.What is the mass of the second body?
A capacitor with capacitance 5μF is charged to5μC. If the plates are pulled apart to reduce the capacitance to 2μF , how much work is done?
A rectangular coil (Dimension5cm × 2.5cm) with 100 turns, carrying a current of 3A in the clock-wise direction, is kept centered at the origin and in the X-Z plane. A magnetic field of 1 T is applied along X-axis. If the coil is tilted through 45º about Z-axis, then the torque on the coil is
The figure shows a Young’s double slit experimental setup. It is observed that when
a thin transparent sheet of thickness t and refractive index µ is put in front of one
of the slits, the central maximum gets shifted by a distance equal to n fringe widths.
If the wavelength of light used is λ,t will be:
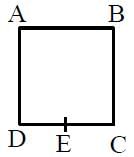
A wire of resistance R is bent to form a square ABCD as shown in the figure. The
effective resistance between E and C is: (E is mid-point of arm CD)
A rigid square loop of side ‘a’ and carrying current I2 is lying on a horizontal surface near a long current I1 carrying wire in the same plane as shown in figure. The net force on the loop due to the wire will be:
The stream of a river is flowing with a speed of 2 km/h. A swimmer can swim at a speed of 4 km/h. What should be the direction of the swimmer with respect to the flow of the river to cross the river straight?
A stationary horizontal disc is free to rotate about its axis. When a torque is applied on it, its kinetic energy as a function of θ , where θ is the angle by which it has rotated, is given as kθ2 . If its moment of inertia is I then the angular acceleration of the disc is:
A system of three charges are placed as shown in the figure:
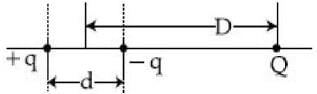
If D > > d, the potential energy of the system is best given by:
An HCl molecule has rotational, translational and vibrational motions. If the rms velocity of HCl molecules in its gaseous phase is 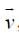 , m is its mass and KBis Boltzman constant, then its temperature will be :
, m is its mass and KBis Boltzman constant, then its temperature will be :
A concave mirror for face viewing has focal length of 0.4 m. The distance at which you hold the mirror from your face in order to see your image upright with a magnification of 5 is:
Determine the charge on the capacitor in the following circuit:




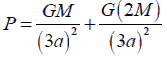
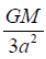

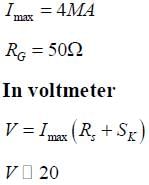
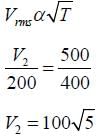
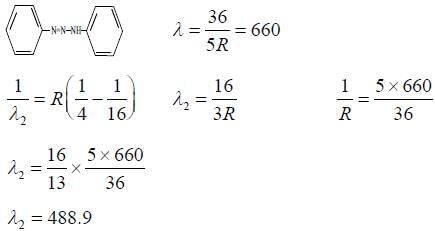
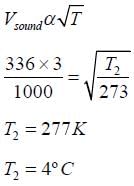
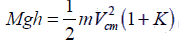

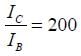
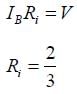
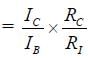
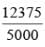 = w + s potential
= w + s potential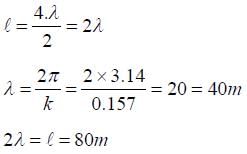
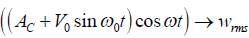
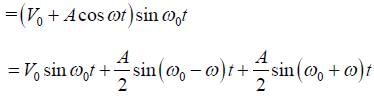
 =D
=D