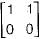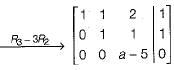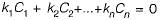Linear Algebra - 1 - Computer Science Engineering (CSE) MCQ
10 Questions MCQ Test - Linear Algebra - 1
If A and B are real symmetric matrices of size n x n. Then, which one of the following is true?
Let a = (aij) be an n-rowed square matrix and I12 be the matrix obtained by interchanging the first and second rows of the n-rowed Identity matrix. Then AI12 is such that its first
Consider the following determinant:

Which of the following is a factor of Δ?
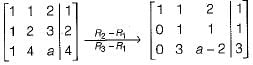
The following system of equations:
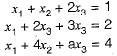
Has a unique solution. The only possible value(s) for a is/are
If M is a square matrix with a zero determinant, which of the following assertion(S) is (are) correct?
S1: Each row of M can be represented as a linear combination of the other rows.
S2: Each column of M can be represented as a linear combination of the other columns.
S3: MX = O has a nontrivial solution.
S4: M has an inverse.
Consider the matrix as given below:
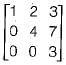
Which one of the following options provides the CORRECT values of the eigenvalues of the matrix?
Consider the following 2 x 2 matrix A where two elements are unknown and are marked by ‘a’ and ‘b'. The eigenvalues of this matrix are -1 and 7. What are the values of ‘a’ and 'b'?



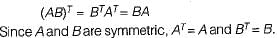

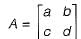


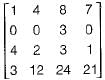
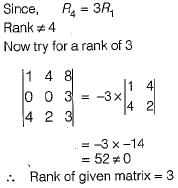
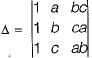
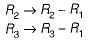
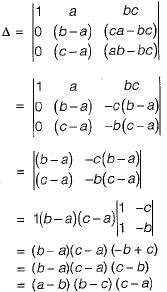
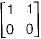 is
is