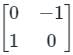Linear Transform MCQ - 1 - IIT JAM MCQ
30 Questions MCQ Test - Linear Transform MCQ - 1
Let T : R2 → R2 be a linear transformation such that T((1, 2)) = (2, 3) and T((0, 1)) = (1, 4).Then T((5, -4)) is
Let V and W be vector spaces over 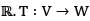 be a map. Then T is a linear transformation iff
be a map. Then T is a linear transformation iff
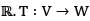 be a map. Then T is a linear transformation iff
be a map. Then T is a linear transformation iff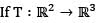 is a linear transformation T(1,0) = (2,3,l) and T(1,1) = (3,0,2) then which one of the following statement is correct?
is a linear transformation T(1,0) = (2,3,l) and T(1,1) = (3,0,2) then which one of the following statement is correct?
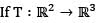 is a linear transformation T(1,0) = (2,3,l) and T(1,1) = (3,0,2) then which one of the following statement is correct?
is a linear transformation T(1,0) = (2,3,l) and T(1,1) = (3,0,2) then which one of the following statement is correct?Let T:R2 -> R2 be the transformation T(x1,x2) = (x1,0). The null space (or kernel) N(T) of T is
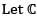 be the vector space of all complex numbers over complex field
be the vector space of all complex numbers over complex field 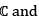
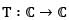 be defined by T(z) =
be defined by T(z) = 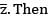
Let T: R3 → R3 be a linear transformation and I be the identify transformation of R3. If there is a scalar C and a non-zero vector x ∈ R3 such that T(x) = Cx, then rank (T – CI)
Which of the following Linear Transformations is not correct for the given matrix?
Consider the basis S = {v1, v2, v3} for 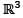 where v1 = (1,1,1) and v2 = (1,1,0), v3 = (1,0,0) and let
where v1 = (1,1,1) and v2 = (1,1,0), v3 = (1,0,0) and let 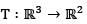 be a linear transformation such that T(v1) = (1,0), T (v2) = (2, -1), T (v3) = (4, 3). Then T (2, - 3, 5) is
be a linear transformation such that T(v1) = (1,0), T (v2) = (2, -1), T (v3) = (4, 3). Then T (2, - 3, 5) is
Which one of the following is not a criterion for linearity of an equation?
Consider the following 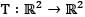 such that T(2,2) = (8, - 6), T (5, 5) = (3, - 2) Then
such that T(2,2) = (8, - 6), T (5, 5) = (3, - 2) Then
Let T be linear transformation on 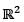 into itself such that T(1,0) = (1,2) and T (1, 1) = (0, 2) .Then T(a, b) is equal to
into itself such that T(1,0) = (1,2) and T (1, 1) = (0, 2) .Then T(a, b) is equal to
If 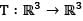 is given by T (x, y, z) = (x - y, y + 3z, x + 2y). Then T-1 is
is given by T (x, y, z) = (x - y, y + 3z, x + 2y). Then T-1 is
Let T: R3 → R3 be a linear transformation and I be the identity transformation of R3. If there is a scalar C and a non-zero vector x ∈ R3 such that T(x) = Cx, then rank (T – CI)
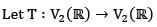 where T be the reflection of the points through the line y = -x then the matrix of T with respect to standard basis is
where T be the reflection of the points through the line y = -x then the matrix of T with respect to standard basis is
Consider the two linear mapsT1 and T2 on V3 defined as T1(x1, x2, x3) = (0, x2, x3) and T2(x1, x2, x3) = (x1, 0,0)
Let T be a linear transformation on the vector space  defined by T(a, b) = (a, 0) the matrix of T relative to the ordered basis {(1,0), (0,1)} of
defined by T(a, b) = (a, 0) the matrix of T relative to the ordered basis {(1,0), (0,1)} of 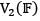 is
is
Let A be an n × n matrix such that the set of all its nonzero eigenvalues has exactly r elements. Which of the following statements is true?
Let 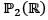 be the polynomial space with basis {1, x, x2} then matrix representation of
be the polynomial space with basis {1, x, x2} then matrix representation of 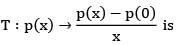
Find the fourier transform of F(x) = 1, |x| < a0, otherwise.
Let T: P3[0,1] →P2[0,1] be defined by T(p(x)) = p"(x) + p'(x). Then the matrix representation of T with respect to basis {1, x, x2, x3} and {1, x, x2} of P3[0,1] and P2[0,1] respectively is
For the standard basis {(1,0,0), (0,1,0), (0,0,1)} of 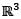 is a linear transformation T from
is a linear transformation T from 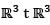 has the matrix representation
has the matrix representation  Then the image of (2,1,2) under T is
Then the image of (2,1,2) under T is
Let us consider a 3×3 matrix A with Eigen values of λ1, λ2, λ3 and the Eigen values of A-1 are?
Let  be the map given by
be the map given by 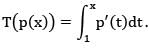 If the matrix of T relative to the standard basis β = γ = {1, x, x2, x3} is
If the matrix of T relative to the standard basis β = γ = {1, x, x2, x3} is 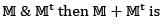
A linear transformation T rotates each vector in 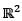 clockwise through 90°. The matrix T relative to standard ordered basis
clockwise through 90°. The matrix T relative to standard ordered basis 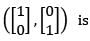




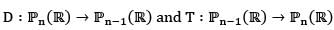 defined by differentiation and integration
defined by differentiation and integration 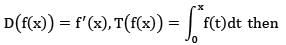
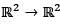 is not a linear mapping?
is not a linear mapping?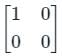 then eigenvalues are 0, 0 ⇒ r = 0
then eigenvalues are 0, 0 ⇒ r = 0