Linear Transform MCQ - 3 - IIT JAM MCQ
30 Questions MCQ Test - Linear Transform MCQ - 3
Let T be a linear operator on a finite dimensional vector space V. If m(λ) = λr + ar-1λr-1 + ... + a1λ + a0 (a0 ≠ 0) be a minimal polynomial of T then
Let {v1,v2, ..., v16} be an ordered basis for 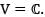 If T is a linear transformation on V defined by T(vi) = vi+1 for 1 < i < 15 and T (v16) = - (v1 + v2 + .... + v16) then
If T is a linear transformation on V defined by T(vi) = vi+1 for 1 < i < 15 and T (v16) = - (v1 + v2 + .... + v16) then
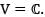 If T is a linear transformation on V defined by T(vi) = vi+1 for 1 < i < 15 and T (v16) = - (v1 + v2 + .... + v16) then
If T is a linear transformation on V defined by T(vi) = vi+1 for 1 < i < 15 and T (v16) = - (v1 + v2 + .... + v16) thenWhich of the following Linear Transformations is not correct for the given matrix?
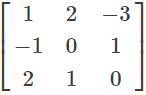
If a eigenvalue of A is λ, then the corresponding eigen value of A−1 is
Let 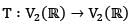 where T be the reflection of the points through the line y = - x then
where T be the reflection of the points through the line y = - x then
Let T be a linear operator on a finite dimensional vector space V. If m(λ) = λr + ar-1λr-1 + ..... + a0λ be a minimal polynomial of T then
Let T be a linear operator on a finite dimensional space V and C is any scalar then C is characteristic value of T if
Let 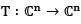 be an linear operator having n distinct eigenvalues. Then
be an linear operator having n distinct eigenvalues. Then
Let V is an n-dimensional vector space over the field 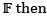 the characteristic polynomial of the identity operator on V is
the characteristic polynomial of the identity operator on V is
Let V be a finite dimensional vector space over the field 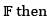 the minimal polynomial for the zero operator is
the minimal polynomial for the zero operator is
Let 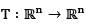 such that T(x1, x2, ...., xn) = (0, x1, x2, ..... xn - 1) then
such that T(x1, x2, ...., xn) = (0, x1, x2, ..... xn - 1) then
If T be a linear operator on a vector space V such that T2 - T + 1 = 0 then
If T : V → V be a linear operator for dim V = n and T has n distinct eigenvalues then
Let A and B he nxn matrices with the same minimal polynomial. Then
Let 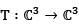 be defined by T(x, y, z) = (x + y + z, -x - y, -x - z) and M be its matrix with respect to standard ordered basis. The matrix M is similar to a matrix which is
be defined by T(x, y, z) = (x + y + z, -x - y, -x - z) and M be its matrix with respect to standard ordered basis. The matrix M is similar to a matrix which is
A matrix M has eigenvalue 1 and 4 with corresponding eigenvectors (1, -1)T and (2,1)T respectively. Then M is
Let V be vector space of real polynomials of degree atmost 2. Define a linear operator 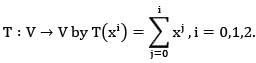 the dimension of the eigenspace of T-1 corresponding to the eigenvalue 1 is
the dimension of the eigenspace of T-1 corresponding to the eigenvalue 1 is
Let A be an n x n matrix from the set of numbers and A3 - 3A2 + 4A - 6I = 0 where I is n x n unit matrix. If A-1 exists then
Let A be n x n matrix which is both Hermitian and unitary, then
Let A be 3 x 3 matrix with real entries such that det(A) = 6 and the trace of A is 0. lf det(A + I) = 0 where I denotes the 3 x 3 identity matrix, then the eigenvalues of A are
It the characteristic root of 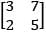 are λ1 and A2, the characteristic roots of
are λ1 and A2, the characteristic roots of 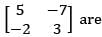
A is any nxn matrix with all entries equal to 1 then 0 is an eigenvalue of A and
Consider the matrix  where a, b and c are non zero real numbers.Then the matrix has
where a, b and c are non zero real numbers.Then the matrix has
Let the characteristic equation of a matrix (x - α)3 + (x - β)3 a be λ2 - λ - 1 then



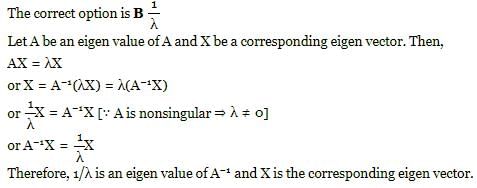
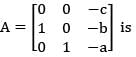
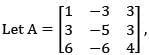 if P is modal matrix for A then P-1 AP is
if P is modal matrix for A then P-1 AP is


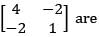
 which of the follow ing is the zero matrix.
which of the follow ing is the zero matrix.















