MCQ (Previous Year Questions) - Binomial Solution (Competition Level 1) - JEE MCQ
30 Questions MCQ Test - MCQ (Previous Year Questions) - Binomial Solution (Competition Level 1)
If the coefficient of (r + 2) th and (3r)th term in the exp. of (1+ x)2n are equal then
[AIEEE 2002]
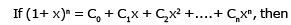
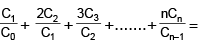
[AIEEE-2002]
The coefficient of x39 in the expansion of 
The number of integral terms in the expansion of
[AIEEE- 2003]
The coefficient of the middle term in the binomial expansion in powers of x of the same if a equals-
[AIEEE 2004]
The coefficient of xn in expansion of (1+x)(1–x)n is
[AIEEE 2004]
[AIEEE 2004]
If the coefficients of rth, (r + 1)th and (r + 2)th terms in the binomial expansion of (1 + y)m are in A.P., then m and r satisfy the equation-
[AIEEE-2005]
If the coefficient of equals the coefficient of
then a and b satisfythe relation
-[AIEEE-2005]
For natural numbers m, n if
In the binomial expansion of (a - b)n, n ≥ 5, the sum of 5th and 6th terms is zero, then a/b equals-
The sum of the series
[AIEEE 2007]
[AIEEE-2008]
The remainder left out when 82n –(62)2n+1 is divided by 9 is -
[AIEEE-2009]
[AIEEE-2010]
The coefficient of x7 in the expansion of (1 – x – x2 + x3)6 is :
[AIEEE-2011]
If n is an positive integer, then
[JEE-MAIN 2013]
The term independent of x in expression of
[JEE-MAIN 2013]
If in the expansion of (1 + x) m ( 1 – x )n, the co-efficients of x and x2 are 3 and – 6 respectively, then m is
[JEE 99,2 ]
Find the largest co-efficient in the expansion of (1 + x)n, given that the sum of co-efficients of the terms in its expansion is 4096.
[REE 2000 (Mains)]
In the binomi al expansion of (a – b)n, n ≥ 5, the sum of the 5th and 6th terms is zero. Then a/b equals.
Find the coefficient of x49 in the polynomial
[REE 2001 (Mains), 3]
is maximum when m is
[JEE 2002 (Scr.)]
Coefficient of t24 in the expansion of (1 + t2)12 (1 + t12) (1 + t24) is
[JEE 2003 (Scr.), 3]
[JEE 2004 (Scr.)]
[JEE 2005 (Scr.)]
The number of seven digit integers, with sum of the digits equal to 10 and formed by using the digits 1, 2 and 3 only, is
[JEE 2009]
For r = 0, 1, ...., 10 l et A r, Br, Cr denote, respectivel y, the coeffi ci ent of x r in the expansions of (1 +
[JEE 2010]
Paragraph for Question Nos. 13 to 14
Let an denote the number of all n-digit positive integers formed by the digits 0, 1 or both such that no consecutive digits in them are 0. Let bn = the number of such n-digit integers ending with digit 1 and cn = the number of such n-digit integers ending with digit 0.
Which of the following is correct ?
[JEE 2012]




















