MCQ (Previous Year Questions) - Continuity And Differentiability (Competition Level 1) - JEE MCQ
24 Questions MCQ Test - MCQ (Previous Year Questions) - Continuity And Differentiability (Competition Level 1)
If f (x) = [x sin p x] { where [x] denotes greatest integer function}, then f (x) is
If for all values of x & y; f(x + y) = f(x) .f(y) and f(5) = 2 f‘ (0) = 3, then f‘ (5) is-
[AIEEE 2002]
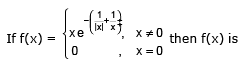
[AIEEE 2003]
Let f(x) = 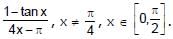 If f(x) is continuous in
If f(x) is continuous in  is -
is -
[AIEEE 2004]
If f is a real-valued differentiable function satisfying | f(x) – f (y) | ≤ (x – y)2, x, y ∈ R and f(0) = 0, then f(1) equals
[AIEEE-2005]
Suppose f(x) is differentiable at x = 1 and
[AIEEE-2005]
The set of points where is differentiable is –
[AIEEE 2006]
The function f : R\{0} → R given by 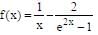 can be made continuous at x = 0 by defining f(0) as
can be made continuous at x = 0 by defining f(0) as
Let f : R → R be a function defined by f(x) = Min {x + 1, |x| + 1}. Then which of the following is true ?
[AIEEE 2007]
Then which one of the following is true ?
[AIEEE 2008]
Let f(x) = x | x | and g(x) = sin x.
Statement – 1 : gof is differentiable at x = 0 and its derivative is continuous at that point.
Statement – 2 :gof is twice differentiable at x = 0.
[AIEEE 2009]
Let f : R → R be a co nti n uo us fu ncti on de fined by f(x) =
The value of p and q for which the function
is continuous for all x in R, are :
[AIEEE 2011]
Consider the function,
Statement 1 : f'(4) = 0
Statement 2: f is continous in [2, 5], differentiable in (2, 5) and f(2) = f(5)
[AIEEE 2012]
If f : R → R is a function defined by where [x] denotes the greates integer function, then f is :
[AIEEE 2012]
The function f(x) = [x] 2 – [x 2] (where [y] is the greatest integer less than or equal to y), is discontinuous at
[JEE 99,2]
Determine the constants a, b & c for which the function f(x) =
x = 0
Let f : R → R be a function defined by, f(x) = max [x, x3]. The set of all points where f(x) is NOT differentiable is
[JEE 2001 (Scr.)]
The left hand derivative of, f(x) = [x] sin ( π x) at x = k, k an integer is (where [ * ] denotes the greatest function)
Which of the following functions is differentiable at x = 0 ?
Let f : R → R be such that f(1) = 3 and f ’(1) = 6.
[JEE 2002 (Scr.), 3]
If f(x) = min. (1, x2, x3), then
[JEE 2006, 5]
m and n are integers m ≠ 0, n > 0 and let p be the left handderivative of .
[JEE 2008, 3]
For every integer n, let an and bn be real numbers. Let function f : IR →IR be given by
for all integers n.
If f is continuous, then which of the folloiwng hold(s) for all n ?
[JEE 2012]














