MCQ: Complementary angles - 1 - SSC CGL MCQ
15 Questions MCQ Test - MCQ: Complementary angles - 1
In the given figure, if AB || CD, then ∠FXE is equal to:


If two angles are complementary of each other, then each angle is:


In the given figure, the value of x, that would make POQ a straight line, is:
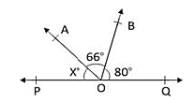

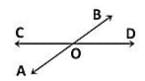
In the given figure, if AOB is a straight line, then the value of x is:
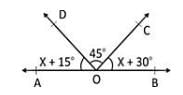
In the given figure, AOB is a straight line. If ∠AOC + ∠BOD = 85°, then ∠COD is:

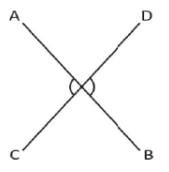
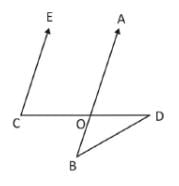
The straight lines AD and BC intersect one another at the point O.
If ∠AOB + ∠BOD + ∠DOC = 274°, then ∠AOC is:
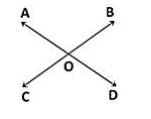
Two straight lines AB and CD cut each other at O. If ∠BOD = 63°, then ∠BOC is:
An angle which is greater than 180° but less than 360° is called:
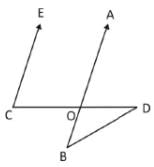
In the figure given below, EC is parallel to AB, ∠ECD = 70° and ∠BDO = 20°. What is the value of ∠OBD?
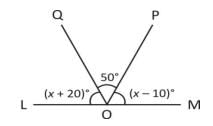
In the figure given below LOM is a straight line. What is the value of x°?
Consider the following statements If two straight lines intersect, then
I. vertically opposite angles are equal.
II. vertically opposite angles are supplementary.
III. adjacent angles are complementary.
Which of the statements given above is/are correct?
If two supplementary angles differ by 44°, then one of the angle is:
In the given figure, line CE is drawn parallel to DB. If ∠BAD = 110°, ∠ABD = 30°, ∠ADC = 75° and ∠BCD = 60°, then the value of x° is: