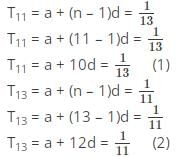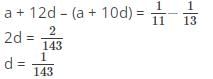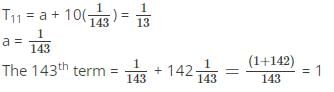Bank Exams Exam > Bank Exams Tests > Quantitative Aptitude/संख्यात्मक योग्यता > MCQ: अंकगणितीय प्रगति - 2 - Bank Exams MCQ
MCQ: अंकगणितीय प्रगति - 2 - Bank Exams MCQ
Test Description
15 Questions MCQ Test Quantitative Aptitude/संख्यात्मक योग्यता - MCQ: अंकगणितीय प्रगति - 2
MCQ: अंकगणितीय प्रगति - 2 for Bank Exams 2025 is part of Quantitative Aptitude/संख्यात्मक योग्यता preparation. The MCQ: अंकगणितीय प्रगति - 2 questions and answers have been
prepared according to the Bank Exams exam syllabus.The MCQ: अंकगणितीय प्रगति - 2 MCQs are made for Bank Exams 2025 Exam. Find important
definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for MCQ: अंकगणितीय प्रगति - 2 below.
Solutions of MCQ: अंकगणितीय प्रगति - 2 questions in English are available as part of our Quantitative Aptitude/संख्यात्मक योग्यता for Bank Exams & MCQ: अंकगणितीय प्रगति - 2 solutions in
Hindi for Quantitative Aptitude/संख्यात्मक योग्यता course. Download more important topics, notes, lectures and mock
test series for Bank Exams Exam by signing up for free. Attempt MCQ: अंकगणितीय प्रगति - 2 | 15 questions in 15 minutes | Mock test for Bank Exams preparation | Free important questions MCQ to study Quantitative Aptitude/संख्यात्मक योग्यता for Bank Exams Exam | Download free PDF with solutions
MCQ: अंकगणितीय प्रगति - 2 - Question 1
एक एपी के पहले चार अंश जिनका a 10 है और d 10 है, क्या होंगे?
Detailed Solution for MCQ: अंकगणितीय प्रगति - 2 - Question 1
Detailed Solution for MCQ: अंकगणितीय प्रगति - 2 - Question 2
Detailed Solution for MCQ: अंकगणितीय प्रगति - 2 - Question 3
MCQ: अंकगणितीय प्रगति - 2 - Question 4
एक अंकगणितीय प्रगति (AP) में, यदि d = -4, a = 28, n = 7, तो a(n) क्या होगा?
Detailed Solution for MCQ: अंकगणितीय प्रगति - 2 - Question 4
MCQ: अंकगणितीय प्रगति - 2 - Question 5
अंत से शुरू करते हुए, A.P. 3, 8, 13, ..., 253 का 20वां पद क्या है?
Detailed Solution for MCQ: अंकगणितीय प्रगति - 2 - Question 5
Detailed Solution for MCQ: अंकगणितीय प्रगति - 2 - Question 6
Detailed Solution for MCQ: अंकगणितीय प्रगति - 2 - Question 7
MCQ: अंकगणितीय प्रगति - 2 - Question 8
एपी 500, 489, 478, 467… -1139 से अंत से 99th क्रम क्या होगा?
Detailed Solution for MCQ: अंकगणितीय प्रगति - 2 - Question 8
MCQ: अंकगणितीय प्रगति - 2 - Question 9
यदि एक एपी के 5वे पद का 5 गुना उसके 15वे पद के 15 गुना के बराबर है, तो उसके 20वे पद का मान क्या होगा?
Detailed Solution for MCQ: अंकगणितीय प्रगति - 2 - Question 9
MCQ: अंकगणितीय प्रगति - 2 - Question 10
यदि किसी अंकगणितीय श्रेणी (AP) का 7वां पद 20 है और इसका 11वां पद 40 है, तो सामान्य अंतर क्या होगा?
Detailed Solution for MCQ: अंकगणितीय प्रगति - 2 - Question 10
Detailed Solution for MCQ: अंकगणितीय प्रगति - 2 - Question 11
Detailed Solution for MCQ: अंकगणितीय प्रगति - 2 - Question 12
MCQ: अंकगणितीय प्रगति - 2 - Question 13
यदि एक एपी का pth पद q है और इसका qth पद p है, तो इसके (p + q)th पद का मूल्य क्या होगा?
Detailed Solution for MCQ: अंकगणितीय प्रगति - 2 - Question 13
Detailed Solution for MCQ: अंकगणितीय प्रगति - 2 - Question 14
MCQ: अंकगणितीय प्रगति - 2 - Question 15
यदि AP की 11वीं पद 1/13 है और इसकी 13वीं पद 1/11 है, तो 143वीं पद का मान क्या होगा?
Detailed Solution for MCQ: अंकगणितीय प्रगति - 2 - Question 15
|
171 docs|185 tests
|
Information about MCQ: अंकगणितीय प्रगति - 2 Page
In this test you can find the Exam questions for MCQ: अंकगणितीय प्रगति - 2 solved & explained in the simplest way possible.
Besides giving Questions and answers for MCQ: अंकगणितीय प्रगति - 2, EduRev gives you an ample number of Online tests for practice