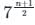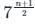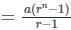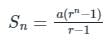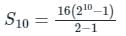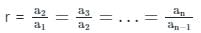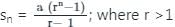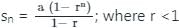MCQ: ज्यामितीय प्रगति - 2 - Bank Exams MCQ
15 Questions MCQ Test - MCQ: ज्यामितीय प्रगति - 2
यदि एक गुणात्मक अनुक्रम (G.P.) का 4था और 5वा पद क्रमशः 2 और 8 हैं, तो पहले 8 पदों का गुणनफल होगा
चार संख्याएँ एक ज्यामितीय प्रगति (GP) बना रही हैं, जिसमें तीसरा पद पहले पद से 9 अधिक है और दूसरा पद चौथे पद से 18 अधिक है। पहला पद क्या है?
यदि पहला पद 125 है और सामान्य अनुपात 2/5 है, तो GP का चौथा पद क्या होगा?
यदि (1/21) + (1/22) + (1/23) .... (1/210) = 1 /k, तो k का मान क्या होगा?
श्रृंखला का योग ज्ञात करें: (20 + 22 + 24 +........+ 28) × 3
फर्श पर गिरने के बाद, एक गेंद उस ऊंचाई का 4/5 हिस्सा वापस उछलती है, जिससे वह गिरी है। यदि इसे 120 मीटर की ऊंचाई से धीरे-धीरे गिराया गया है, तो यह निर्धारित करें कि यह कुल कितनी दूरी तय करती है जब तक कि यह स्थिर नहीं हो जाती।
संख्याओं 7, 72, 73, _________ 7n का ज्यामितीय औसत क्या है?
एक जी.पी. के 10वें पद और 7वें पद का अनुपात 1 ∶ 8 है। जी.पी. का समान अनुपात क्या है?
गणितीय अनुक्रम का तीसरा पद 16 है। इसके पहले पाँच पदों का गुणनफल क्या है?
16, 32, 64, 128,...... इस श्रंखला के पहले 10 अंशों का योग क्या है?
यदि G r सेटों के अवलोकनों के उत्पाद का ज्यामितीय माध्य है। ज्यामितीय माध्य G1, G2, G3, ……………, Gr क्रमशः हैं, तो G का मान क्या है?
तीन दोस्तों अल्फा, बीटा और गामा की उम्र ज्यामितीय प्रगति (G.P.) में है और उनकी उम्र का योग 57 है और उनका गुणनफल 5832 है। उनकी उम्र क्या हैं?
यदि GP 5, 10, 20, ... के n संख्याओं का योग 1275 है, तो n कितना है?