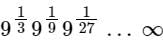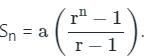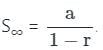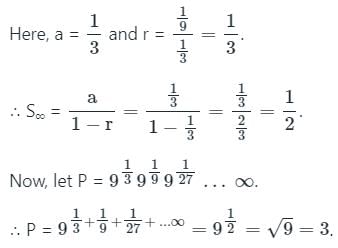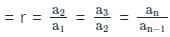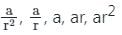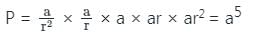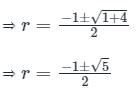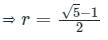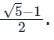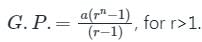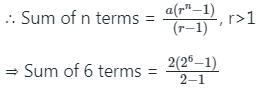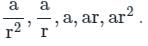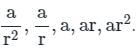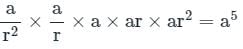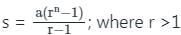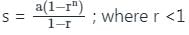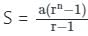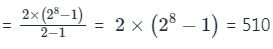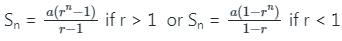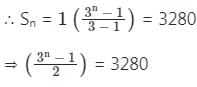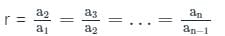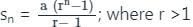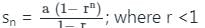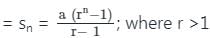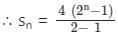MCQ: ज्यामितीय प्रगति - 3 - Bank Exams MCQ
15 Questions MCQ Test - MCQ: ज्यामितीय प्रगति - 3
यदि एक संक्रामक प्रगति (G.P.) के 4th, 7th और 10th पद क्रमशः a, b, c हैं, तो a, b, c के बीच का संबंध क्या है?
यदि 21/e, 2b/ac, 21/a जीपी में हैं, तो निम्नलिखित में से कौन सा सही है?
एक जी.पी. में, 5वां पद 96 है और 8वां पद 768 है, तो जी.पी. का 3रा पद क्या है?
यदि जीपी 5, 10, 20, ... के n अंकों का योग 1275 है, तो n क्या होगा?
एक G.P. में सकारात्मक पदों के लिए, यदि प्रत्येक पद अगले दो पदों के योग के बराबर है। तो G.P. का सामान्य अनुपात क्या होगा?
एक जी.पी. (गुणात्मक अनुक्रम) का तीसरा पद 3 है। इसके पहले पांच पदों का गुणनफल क्या है?
एक जी.पी. के शर्तें सकारात्मक हैं। यदि प्रत्येक शर्त उसके बाद आने वाली दो शर्तों के योग के बराबर है, तो सामान्य अनुपात क्या है?
यदि किसी जी.पी. का nth पद 2n है, तो इसके पहले 6 पदों का योग ज्ञात करें।
गणितीय प्रगति का तीसरा पद 9 है। इसके पहले पांच पदों का गुणनफल क्या है?
किस संभावित मान के लिए x, संख्याएँ - 2/7, x, - 7/2 एक GP (ज्यामितीय प्रगति) में हैं?
एक व्यक्ति के 2 माता-पिता, 4 दादा-दादी, 8 परदादा-दादी और इसी तरह हैं। उसके अपने पूर्वजों की 8 पीढ़ियों में कुल पूर्वजों की संख्या ज्ञात करें।
श्रृंखला 1 + 3 + 32 + ... के लिए, n पदों का योग 3280 है। n का मान ज्ञात करें।
यदि GP 4, 8, 16, ... के n अंकों का योग 2044 है, तो n क्या होगा?


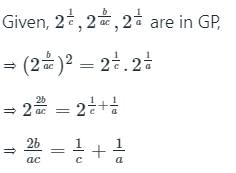

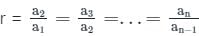
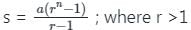
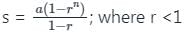
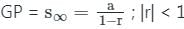
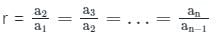
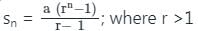
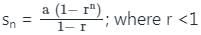
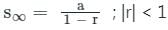
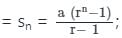 जहाँ r >1
जहाँ r >1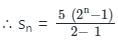
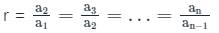
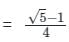
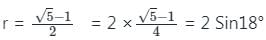 मिलता है।
मिलता है।