MCQ: विश्लेषण (विश्लेषणात्मक तर्क) - 2 - RRB NTPC/ASM/CA/TA MCQ
15 Questions MCQ Test General Intelligence & Reasoning for RRB NTPC (Hindi) - MCQ: विश्लेषण (विश्लेषणात्मक तर्क) - 2
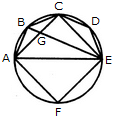
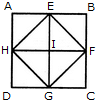
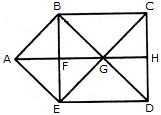
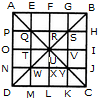
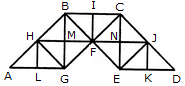
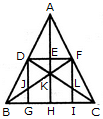
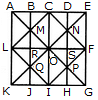
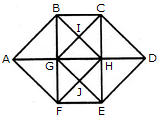
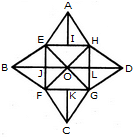
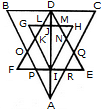
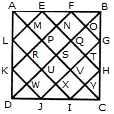
दी गई आकृति में त्रिकोणों की संख्या ज्ञात करें।
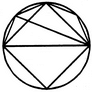

दी गई आकृति में त्रिकोणों की संख्या ज्ञात करें।
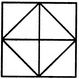

दी गई आकृति में त्रिकोणों की संख्या ज्ञात करें।
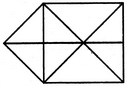

दी गई आकृति में त्रिकोणों की संख्या ज्ञात करें।

दी गई आकृति में त्रिकोणों की संख्या ज्ञात करें।
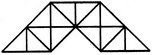
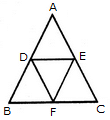
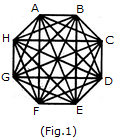
दी गई आकृति में सीधी रेखाओं की संख्या और त्रिकोणों की संख्या क्या है।
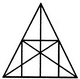
दी गई आकृति बनाने के लिए आवश्यक न्यूनतम सीधी रेखाओं की संख्या ज्ञात करें।
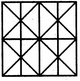
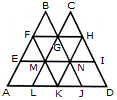
दिए गए चित्र में त्रिकोणों की संख्या खोजें।
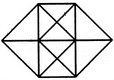
दी गई आकृति में त्रिकोणों की संख्या ज्ञात करें।
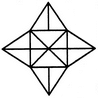
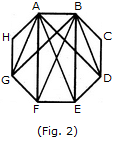
दिए गए आकृति में त्रिकोणों की संख्या ज्ञात करें।
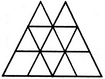
दी गई आकृति में त्रिकोणों की संख्या ज्ञात करें।
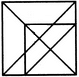
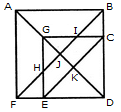
दिए गए चित्र में त्रिकोणों की संख्या ज्ञात कीजिए।
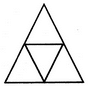
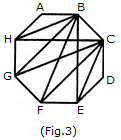
दी गई आकृति में त्रिकोणों की संख्या ज्ञात करें।
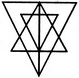
ऐसे कितने त्रिकोण बनाए जा सकते हैं जिनके शीर्षक अष्टभुज के शीर्षों से हों लेकिन जिनमें से केवल एक भुजा अष्टभुज के साथ सामान्य हो?
दी गई आकृति में त्रिकोणों की संख्या ज्ञात करें।

|
127 docs|197 tests
|
|
127 docs|197 tests
|