MCQ: सही प्रिज्म - Bank Exams MCQ
10 Questions MCQ Test Quantitative Aptitude/संख्यात्मक योग्यता - MCQ: सही प्रिज्म
एक प्रिज्म का आधार एक समकोण त्रिकोण है जिसका कर्ण 3√2 सेमी है। यदि प्रिज्म की ऊँचाई 12 सेमी है, तो प्रिज्म का आयतन ज्ञात कीजिए?
एक प्रिज्म का आधार नियमित हेक्सागोनल है जिसकी भुजा 12 सेंटीमीटर है। यदि प्रिज्म का कुल सतही क्षेत्रफल 1024√3 सेंटीमीटर2 है, तो प्रिज्म की ऊँचाई (सेंटीमीटर में) क्या होगी?
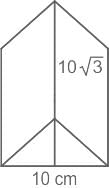
एक समकर्ण त्रिभुज जिसका भुजा 10 सेमी है, एक सीधे प्रिज्म का आधार है। यदि इस प्रिज्म की ऊँचाई 10√3 सेमी है, तो प्रिज्म का कुल सतही क्षेत्रफल क्या होगा?
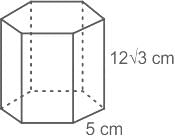
एक सही प्रिस्म का आधार एक नियमित षट्भुज है, जिसका पक्ष 5 सेमी है। यदि इसकी ऊँचाई 12√3 सेमी है, तो इसका आयतन (सेमी3) क्या होगा:
एक वर्ग प्रिज्म का सतह क्षेत्रफल ज्ञात करें, जिसकी भुजा 2 सेमी और ऊँचाई 4 सेमी है।
एक प्रिज्म का सामान्य हेक्सागोनल आधार है जिसकी भुजा 8 सेमी है और प्रिज्म का कुल सतही क्षेत्रफल 912√3 सेमी2 है, तो प्रिज्म की ऊँचाई क्या है?
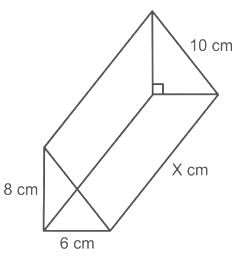
एक समकोण त्रिकोणीय प्रिज्म की पार्श्व सतह क्षेत्रफल 288 cm2 है। यदि छोटे आधारों की लंबाई क्रमशः 6 cm और 8 cm है, तो प्रिज्म की ऊँचाई ज्ञात करें।
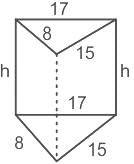
एक सही प्रिज्म का आधार एक त्रिकोण है, जिसकी भुजाएँ 8 सेमी, 15 सेमी और 17 सेमी हैं, और इसकी पार्श्व सतह क्षेत्र 480 सेमी2 है। प्रिज्म का आयतन (सेमी3 में) क्या है?
|
171 docs|185 tests
|