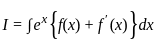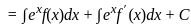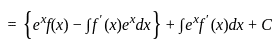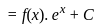MPTET Varg 1 Mathematics Mock Test - 2 - MPTET MCQ
30 Questions MCQ Test - MPTET Varg 1 Mathematics Mock Test - 2
हमेशा बहुवचन में प्रयुक्त होने वाला शब्द है:
"लक्ष्मी + छाया" का संधि-पद निम्नलिखित में से किस संधि का सही उदाहरण होगा?
Select the most appropriate article to fill in the blank. If an article is not needed, then select 'no article'.
Can you lend me ______ couple of books?
In which of the following city the first bone bank of Madhya Pradesh being set up?
When did the Indian Constitution come into effect?
The series given below contains a sequence of alphabets and numbers. Identify the INCORRECT combination:
i. 858plo7op7 ii. 858plo7op07 iii. 858plo7op7 iv. 858plo7op7
Which type of memory is also called as 'inactive memory?
A plan prepared keeping in view of the lessons to be taught month wise in an academic year is called
Dyspraxia is a condition in which children have problems with:
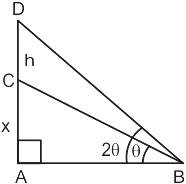
A vertical tower stands on a horizontal plane and is surmounted by a vertical flagstaff of height h. At a point on the plane the angles of elevation of the bottom and top of the flagstaff are θ and 2θ respectively. What is the height of the tower ?
Set A has 3 elements and the set B has 4 elements. Then the number of injective mappings that can be defined from A to B is
The values of k for which y = x2 + kx + 16 touches the x-axis are:
If α, β are the roots of the quadratic equation x2 - 11x + 18 = 0, then the value of α2 + β2 is:
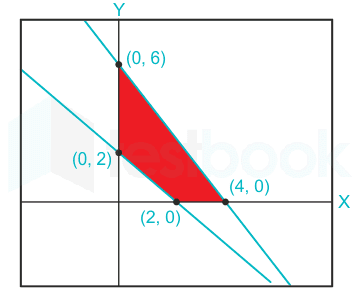
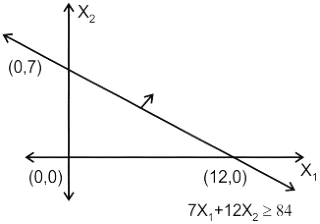
The point which does not lie in the half plane of the given constraint of a linear programming problem will be? The constraint is given as,
7x1 + 12x2 ≥ 84
Let W be the set of all triples (x1, x2, x3) of real numbers that satisfy the equation 2x1 - x2 + 3x3 = k. If W is to be a vector space, then the value of k is:
Two coins tossed together find the probability of getting at least 1 tail?
Let A be n × n matrix over R. Consider the following statements
I. Rank A = n
II. Det (A) ≠ 0
Then,
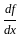 is continuous at x = 0 is
is continuous at x = 0 is
The angle of elevation of the top of a tower from a point on the ground is 30°. After walking 30 meters towards the tower, the angle of elevation of the top becomes 60°. Find the height (in meters) of the tower.
Maximize z = 4x + 6y
subject to
3x + 2y ≤ 12, x + y ≥ 2, x, y ≥ 0





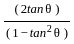
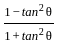
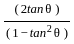 = (x + h)/AB [Using formula (2)]
= (x + h)/AB [Using formula (2)]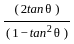 =
= 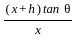 [From equation (1)]
[From equation (1)]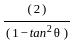 =
= 
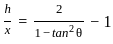
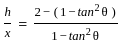
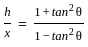
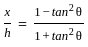 = cos2θ [Using formula (3)]
= cos2θ [Using formula (3)]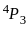
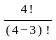
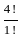
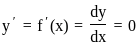 at the maxima/minima.
at the maxima/minima.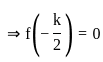
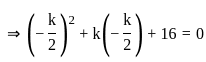
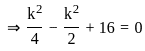
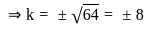 .
.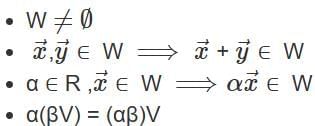
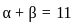
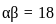
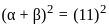
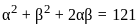
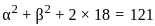
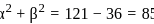
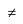
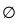
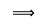 x + y ∈ W
x + y ∈ W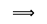 α.x ∈ W
α.x ∈ W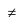
 , for if k = 1,2,-1
, for if k = 1,2,-1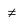
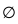 to be a subspace .
to be a subspace .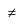
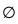
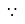
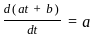
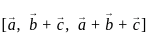 is
is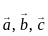 are any non-zero vector then
are any non-zero vector then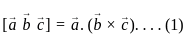

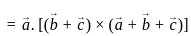
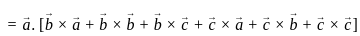
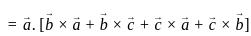
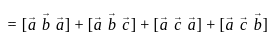
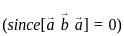
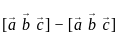
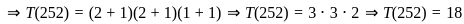
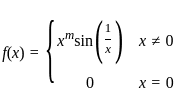
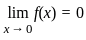
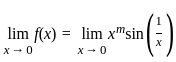
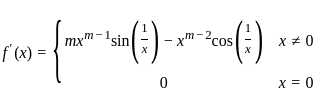
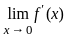 should be continuous
should be continuous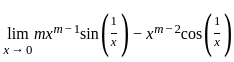
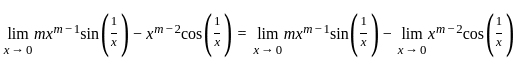
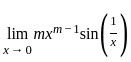 will be zero for all values of m > 1
will be zero for all values of m > 1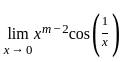 will be zero for all values of m > 2
will be zero for all values of m > 2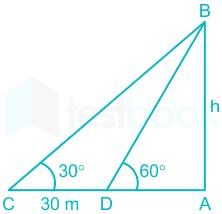
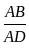 = tan60° = √3
= tan60° = √3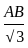
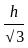
 = tan30° =
= tan30° = 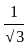
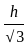
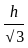 = 30
= 30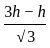 = 30
= 30
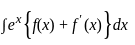 is equal to
is equal to