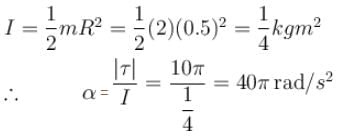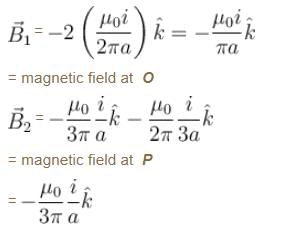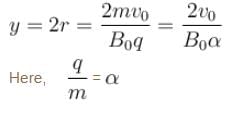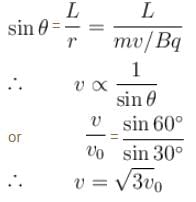Magnetic Effect Of Current NAT Level - 2 - Physics MCQ
10 Questions MCQ Test Topic wise Tests for IIT JAM Physics - Magnetic Effect Of Current NAT Level - 2
A charged particle enters a uniform magnetic field with velocity vector at an angle of 45° with the magnetic field. The pitch of the helical path followed by the particle is p. The radius of the helix is given by p/nπ. The value of n is
A copper wire of diameter 1.6 mm carries a current i. The maximum magnetic field due to this wire is 5 × 10–3 T. The value of i is :
The magnetic field at the centre of an equilateral triangular loop of side 2L and carrying a current i is given by 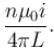
Find the value of n ____.
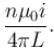
Find the value of n ____.
Ratio of magnetic field at the centre of a current carrying coil of radius R and at a distance of 3R on its axis is :
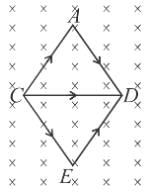
Same current i = 2A is flowing in a wire frame as shown in figure. The frame is a combination of two equilateral triangles ACD and CDE of side 1m. It is placed in uniform magnetic field B = 4T acting perpendicular to the plane of frame. The magnitude of magnetic force acting on the frame is :
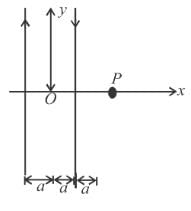
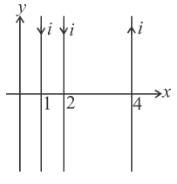
Equal currents i = 1 A are flowing through the wires parallel to y-axis located at x = +1m, x = +2, x = +4m etc, but in opposite directions as shown. The magnetic field at origin (in units of 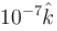 tesla) will be :
tesla) will be :
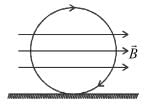
A conducting ring of mass 2 kg and radius 0.5 m is placed on a smooth horizontal plane. The ring carries a current i = 4A. A horizontal magnetic field B = 10 T is switched on at time t = 0 as shown in figure. The initial angular acceleration (in rad/s2) of the ring will be
Two parallel wires carrying equal currents in opposite directions are placed at x = +a parallel to y-axis with z = 0. Magnetic field at origin O is B1 and at P (2a, 0, 0) is B2. Then the ratio B1/B2 is :
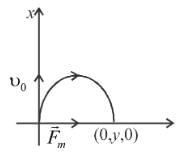
A particle of charge per unit mass α is released from origin with a velocity 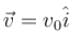 in a uniform magnetic field
in a uniform magnetic field 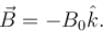 If the particle passes through (0, y, 0), then y is equal to
If the particle passes through (0, y, 0), then y is equal to  The value of n is ____.
The value of n is ____.
A charged particle is projected with velocity v0 along positive x-axis. The magnetic field B is directed along negative z-axis between x = 0 and x = L. The particle emerges out (at x = L) at an angle of 60° with the direction of projection. Find the velocity with which the same particle is projected (at x = 0) along positive x-axis so that when it emerges out (at x = L), the angle made by it is 30° with the direction of projection is nv0. Find the value of n.


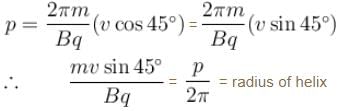
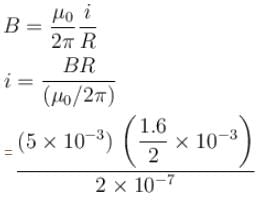

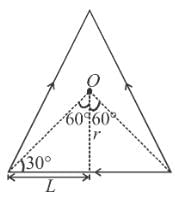
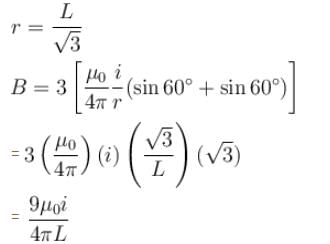



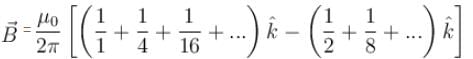
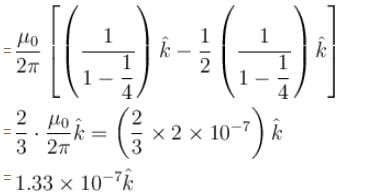



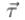 i.e., axis of rotation in the y-axis. Moment of inertia about which is
i.e., axis of rotation in the y-axis. Moment of inertia about which is