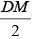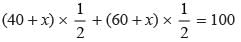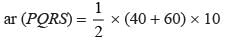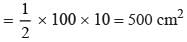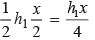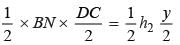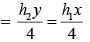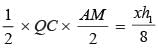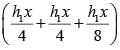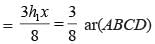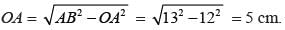Math Olympiad Test: Area of Parallelograms and Triangles- 2 - Class 9 MCQ
15 Questions MCQ Test - Math Olympiad Test: Area of Parallelograms and Triangles- 2
If a triangle and a parallelogram are on the same base and between the same parallels, and area of triangle is A, then area of parallelogram is:
ABCD is a parallelogram
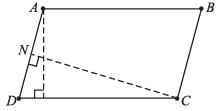
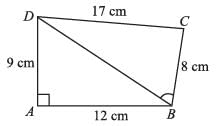
AM = 7 cm, CN = 8 cm and AB = CD = 10 cm, Find AD.

AM = 7 cm, CN = 8 cm and AB = CD = 10 cm, Find AD.
P, Q, R and S are the midpoints of DC, BC, AB and AD respectively. area of parallelogram PQRS is

The median of a triangle divides is into two:
If AD is median of ∆ABC and P is a point on AC such that ar(∆ADP) : ar(∆ABD) = 2 : 3, then ar(∆PDC) : ar(∆ABC) is
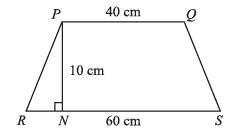
ABCD is a trapezium in which AB ∥ CD and CD = 40 cm, and AB = 60 cm. If X and Y are, respectively, the mid points of AD and BC, then XY =
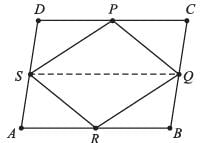
Area of trapezium, PQRS in the given figure is:
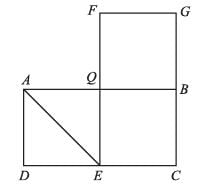
Find the area of quadrilateral ABCD
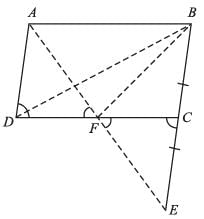
ABCD is a parallelogram in which BC is produced to E such that CE = BC. AE intersects CD at F. If area ∆DFB = 3 cm2, area of parallelogram ABCD is:
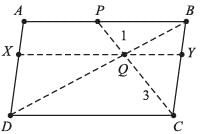
ABCD and FECG are parallelograms equal in area. If ar(∆AQE) = 12cm2, then ar(parallelogram FGBQ) =
ABCD is a parallelogram. P is the midpoint of AB. BD and CP intersect at Q such that QC : QP = 3 : 1. If the ar(∆PBQ) = 10 cm2, then area of parallelogram ABCD is:
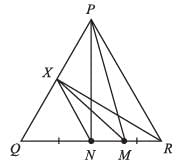
M is a point on base QR of ∆PQR, and N is the midpoint of QR. NX is drawn parallel to MP at X. If ar(∆PQR) = 12cm2, then ar(∆XMR) =
ABCD is a parallelogram, P and Q are the mid-points of BC and CD respectively, then, ar(∆APQ) = K (ar(ABCD)), K =
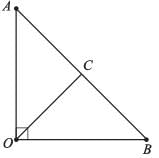
∠AOB = 90°, AC = BC, OA = 12 cm and OC = 6.5 cm. The area (in cm2) of ∆AOB is:


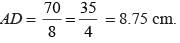


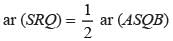
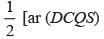 + ar (ASQB)]
+ ar (ASQB)]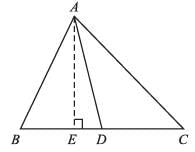
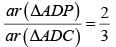
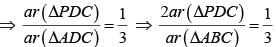
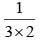 = 1 : 6
= 1 : 6 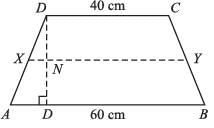
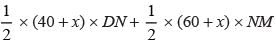
 …(i)
…(i)