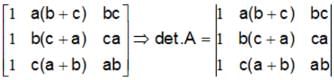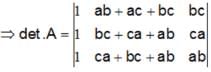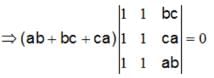Mathematics: CUET Mock Test - 2 - CUET MCQ
30 Questions MCQ Test - Mathematics: CUET Mock Test - 2
Find the general solution of the differential equation 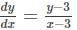 (x, y≠3).
(x, y≠3).
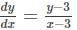 (x, y≠3).
(x, y≠3).Find the general solution of the differential equation 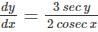 .
.
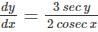 .
.Find the general solution of the differential equation 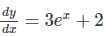
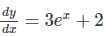
Find the particular solution of the differential equation 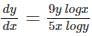 .
.
If  is skew symmetric matrix, then value of x2 + y2 + z2 + u2 + v2 + w2 is:
is skew symmetric matrix, then value of x2 + y2 + z2 + u2 + v2 + w2 is:
Let A = 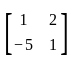 and A-1 = xA + yI, then value of x and y are
and A-1 = xA + yI, then value of x and y are
Statement 1: In a Poisson distribution, events can occur any number of times during a specified period.
Statement 2: The probability of one event happening is dependent on the occurrence of another event in the same period.
Which of the statements given above is/are correct?
A particle moves with uniform acceleration along a straight line and describes distances 21m, 43m and 91m at times 2, 4 and 7 seconds, respectively.What is the velocity of the particle in 3 seconds?
The distance x of a particle moving along a straight line from a fixed point on the line at time t after start is given by t = ax2 + bx + c (a, b, c are positive constants). If v be the velocity of the particle and u(≠0) be the initial velocity of the particle then which one is correct?
A particle is moving in a straight line and its distance x from a fixed point on the line at any time t seconds is given by, x = t4/12 – 2t3/3 + 3t2/2 + t + 15. What is the minimum velocity?
If the curves x2/a + y2/b = 1 and x2/c + y2/d = 1 intersect at right angles, then which one is the correct relation?
(a1, a2) ∈R implies that (a2, a1) ∈ R, for all a1, a2∈A. This condition is for which of the following relations?
P(x; μ) = (e-μ) (μx) / x! is the formula for _____
What will be the value of x + y + z if cos-1 x + cos-1 y + cos-1 z = 3π?
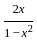 ) with respect to sin-1(
) with respect to sin-1(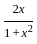 ) is equal to
) is equal to
Match List-I with List-II:
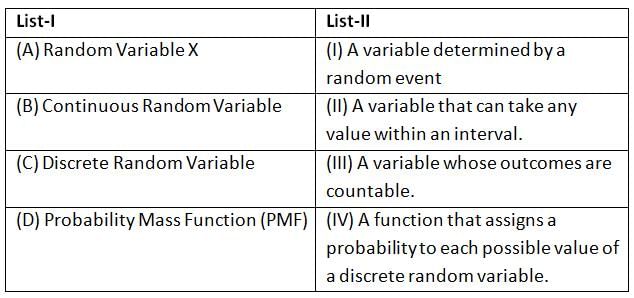
Choose the correct answer from the options given below:
Match List-I with List-II:
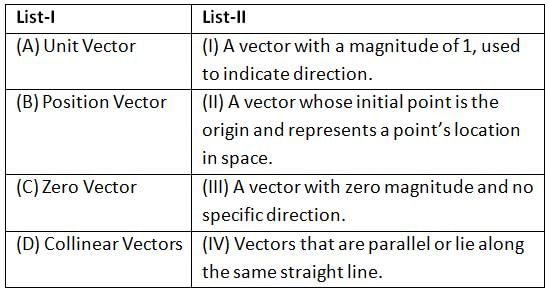
Choose the correct answer from the options given below:
Find the particular solution of the differential equation 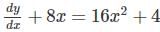 given that y = 1/3 when x = 1.
given that y = 1/3 when x = 1.
Find the unit vector in the direction of vector where P and Q are the points (1, 2, 3) and (4, 5, 6), respectively
A particle moves in a horizontal straight line under retardation kv3, where v is the velocity at time t and k is a positive constant. If initial velocity be u and x be the displacement at time,then which one is correct?
The distance s of a particle moving along a straight line from a fixed-pointO on the line at time t seconds after start is given by x = (t – 1)2(t – 2)2. What will be the distance of the particle from O when its velocity is zero?


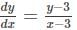
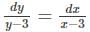
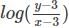 = logC1
= logC1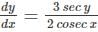
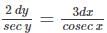

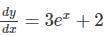
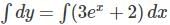 -----(1)
-----(1)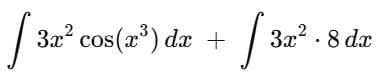
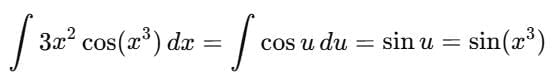
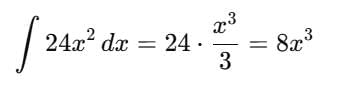
 .... (1)
.... (1)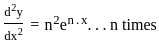
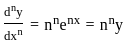
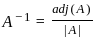 where adj(A) is called an adjoint matrix.
where adj(A) is called an adjoint matrix.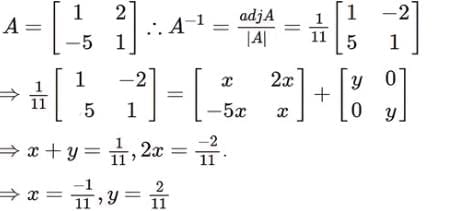
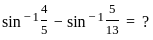
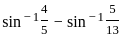

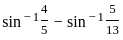
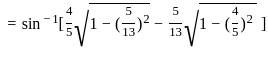
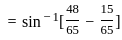
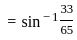
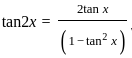
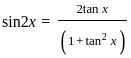
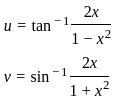
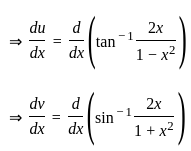

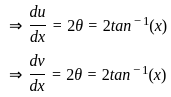
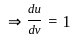
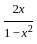
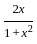
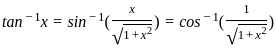
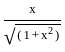 )
)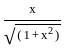 , since sin(sin
, since sin(sin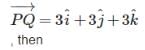
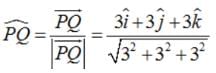
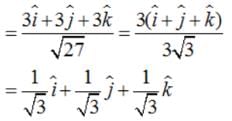
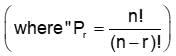
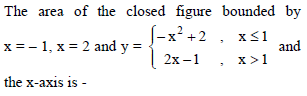
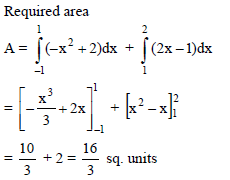
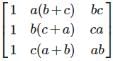 , then Det. A is
, then Det. A is