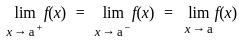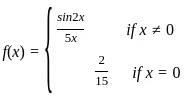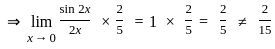To find the smallest value of the polynomial
f(x) = x³ - 18x² + 96 on the interval [0, 9], follow these steps:
Step 1: Find the derivative
To locate critical points, we differentiate the function:
f'(x) = 3x² - 36x
Step 2: Set the derivative equal to zero
3x² - 36x = 0
Factor the expression:
3x(x - 12) = 0
This gives two critical points:
x = 0 and x = 12
Step 3: Check which points lie in the interval [0, 9]
Since x = 12 is outside the interval, we only consider:
-
x = 0
-
x = 9 (right endpoint of the interval)
Step 4: Evaluate f(x) at x = 0 and x = 9
-
f(0) = 0³ - 18(0)² + 96 = 96
-
f(9) = 9³ - 18(9)² + 96
= 729 - 1458 + 96
= -633
Step 5: Conclusion
The smallest value of the function on [0, 9] is:
-633 at x = 9


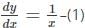
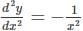
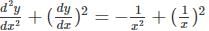
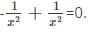

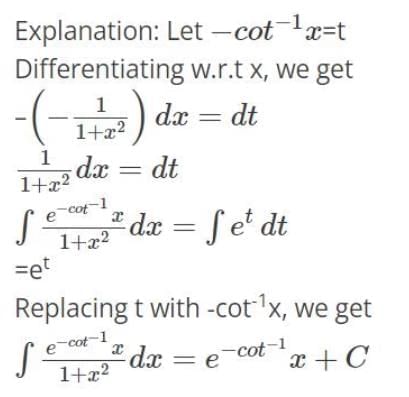
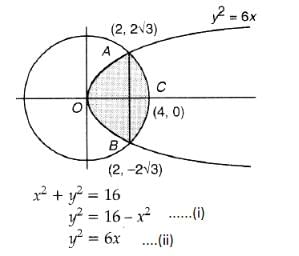


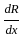
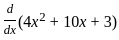
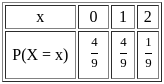
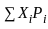 =
= 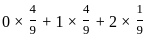 =
= 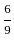
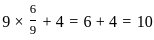
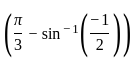 :
: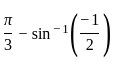
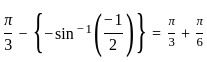
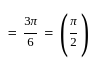
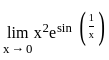 ?
?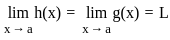 , then
, then 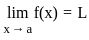 .
.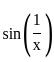 ≤ 1
≤ 1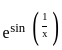 ≤ e1
≤ e1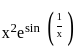 ≤ x2e
≤ x2e
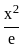 , f(x) =
, f(x) = 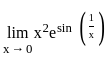 and g(x) = x2e.
and g(x) = x2e.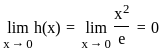 .
.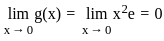 .
.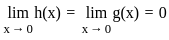 , we must have
, we must have 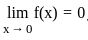 .
.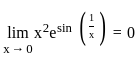 .
.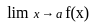 exists if
exists if 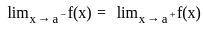
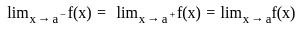
 is continuous at x = 0
is continuous at x = 0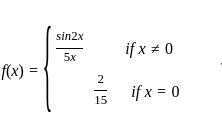
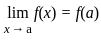 exists or its graph is a single unbroken curve.
exists or its graph is a single unbroken curve.