Mathematics: CUET Mock Test - 6 - CUET MCQ
30 Questions MCQ Test - Mathematics: CUET Mock Test - 6
In what ratio did Sitaram lent the money at 6% p.a. and 10% p.a. respectively?
What amount of money is lent at 10% p.a. simple interest?
What is the ratio of the interest paid by Shyam and Sushil respectively
The probability that a person stopping at a gas station will ask to have his tyres checked is 0.12, the probability that he will ask to have his oil checked is 0.29 and the probability that he will ask to have them both checked is 0.07. The probability that a person who has his tyres checked will also have oil checked is
A bike manufacturing factory has two plants P and Q. Plant P manufactures 60 percent of bikes and plant Q manufacture 40 percent. 80 percent of the bikes at plant P and 90 percent of the bikes at plant Q are rated of standard quality. A bike is chosen at random and is found to be of standard quality. What is the probability that it has come from plant P?
What will be the value of x + y + z if cos-1 x + cos-1 y + cos-1 z = 3π?
If the order of the matrix is m×n, then how many elements will there be in the matrix?
The matrix which follows the conditions m=n is called?
Which of the following matrices will not have a determinant?
Which of the following is a matrix of the order 2×2 where the equation of the elements is given by aij =i+j.
Consider the matrix A= 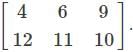 What is the type of matrix?
What is the type of matrix?
Which of the following relations is symmetric but neither reflexive nor transitive for a set A = {1, 2, 3}.
What is the value of sin-1(-x) for all x belongs to [-1, 1]?
Which of the following relations is transitive but not reflexive for the set S={3, 4, 6}?
What is the value of r = 1Σn f(x) if f(r) = 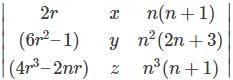 where n € N?
where n € N?
What is the value of cos-1(-x) for all x belongs to [-1, 1]?
Which one is correct, the following system of linear equations 2x – 3y + 4z = 7, 3x – 4y + 5z = 8, 4x – 5y + 6z = 9 has?


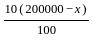
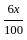 +
+ 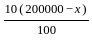 = 18000 (given)
= 18000 (given)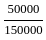 = 1 ∶ 3
= 1 ∶ 3
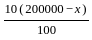
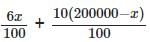 = 18000 (given)
= 18000 (given)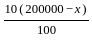
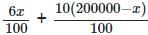 = 18000 (given)
= 18000 (given)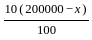
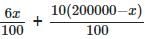 = 18000 (given)
= 18000 (given)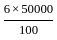 = Rs. 3000
= Rs. 3000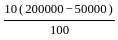 = Rs. 15000
= Rs. 15000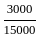 = 1 ∶ 5
= 1 ∶ 5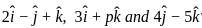 are coplanar then value of p is ?
are coplanar then value of p is ?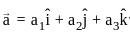 ,
, 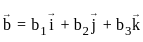 and
and 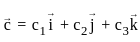 , then
, then 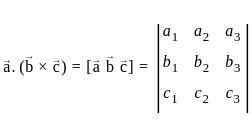 .
.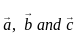 vectors are coplanar then
vectors are coplanar then 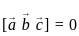
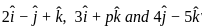 are coplanar.
are coplanar.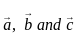 vectors are coplanar then
vectors are coplanar then 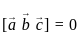
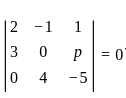
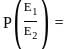 Probability o fgetting the event E1 when E2 is already occured.
Probability o fgetting the event E1 when E2 is already occured.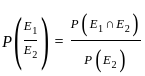
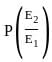 = Probability of person who has his tyre checked will also have oil checked
= Probability of person who has his tyre checked will also have oil checked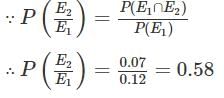
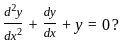
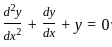
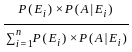 , i = 1, 2, ... n
, i = 1, 2, ... n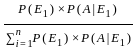 , i = 1, 2, ... n
, i = 1, 2, ... n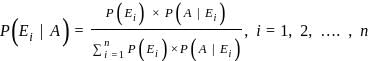
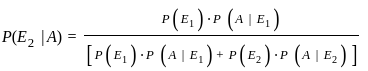
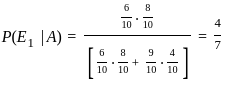
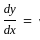 amemx - mbe-mx
amemx - mbe-mx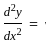 am2emx + bm2e-mx
am2emx + bm2e-mx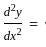
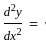
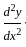 -
-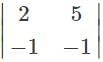 .
.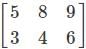 is not possible as it is a rectangular matrix and not a square matrix. Determinants can be calculated only if the matrix is a square matrix.
is not possible as it is a rectangular matrix and not a square matrix. Determinants can be calculated only if the matrix is a square matrix.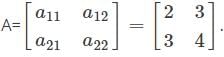
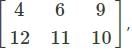 m = 3 and n = 2 i.e.
m = 3 and n = 2 i.e.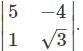
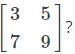
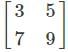 is 2. Therefore, the order of the matrix is 2×2(m×n).
is 2. Therefore, the order of the matrix is 2×2(m×n). is ____
is ____ is of the order 3×1. The matrix has only one column (n=1). Hence, it is a column matrix.
is of the order 3×1. The matrix has only one column (n=1). Hence, it is a column matrix.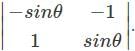
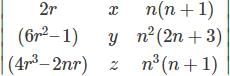

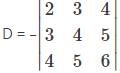
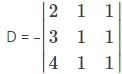

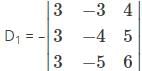
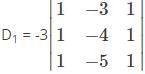
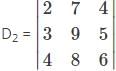
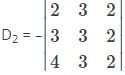
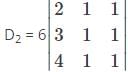
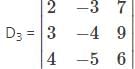
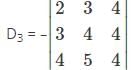
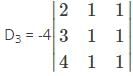
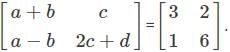
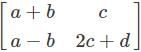 and
and 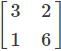 are equal matrices. Comparing the two matrices, we get a+b=3, c=2, a-b=1, 2c+d=6
are equal matrices. Comparing the two matrices, we get a+b=3, c=2, a-b=1, 2c+d=6















