Mathematics: CUET Mock Test - 8 - CUET MCQ
30 Questions MCQ Test - Mathematics: CUET Mock Test - 8
Match List-I with List-II:
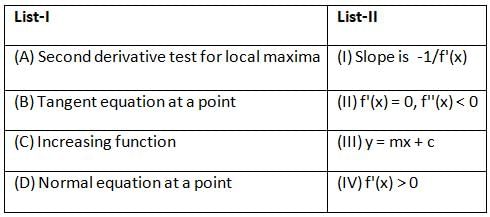
Choose the correct answer from the options given below:

Choose the correct answer from the options given below:
Find the value of x, y, z for the given system of equations.
2x+3y+2z=50
x+4y+3z=40
3x+3y+5z=60
2x+3y+2z=50
x+4y+3z=40
3x+3y+5z=60
If X is a binomial variate with the range {0,1,2,3,4,5,6} and P(X=2) = 4P(X=4), then the parameter P of X is
Probability that A speaks truth is 5/9 . A coin is tossed and reports that a head appears. The probability that actually there was head is:
A man is known to speak truth 3 out of 4 times. He throws a die and reports that it is a six. Find the probability that it is actually a six.
In a transportation problem rows are the supply points and columns are the demand points. If total supply is less than total demand then
If the numbers of sources are 6 and the number of destinations are 7. The total number of non-redundant constraints in linear programming problem formulation is ___________
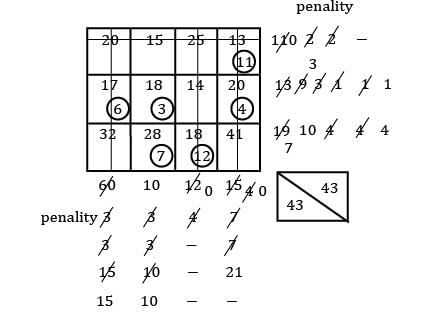
Determine the initial basic feasible solution of the following transportation problem by using VAM.

Find a vector in the direction of the vector which has a magnitude of 8 units
In the following case, determine whether the given planes are parallel orperpendicular, and in case they are neither, find the angles between them. 2x + y + 3z – 2 = 0 and x – 2y + 5 = 0
If the rate of change of radius of a circle is 6 cm/s then find the rate of change of area of the circle when r=2 cm.
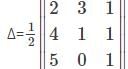
Find the area of the triangle with the vertices (2,3), (4,1), (5,0).
Find the value of k for which the points (3, 2), (1, 2), (5, k) are collinear.
For which of the following element in the determinant Δ= 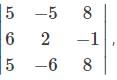 the minor and the cofactor both are zero.
the minor and the cofactor both are zero.
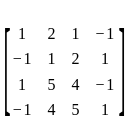
Consider the matrix  . Which of the following is/are true?
. Which of the following is/are true?
Match List-I with List-II:
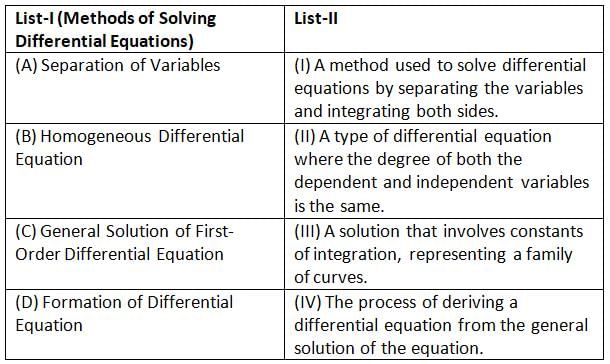
Choose the correct answer from the options given below:
A given systems of equations is said to be inconsistent if _____


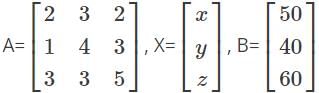
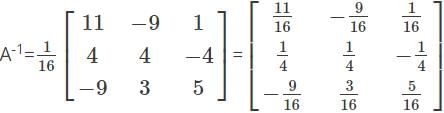
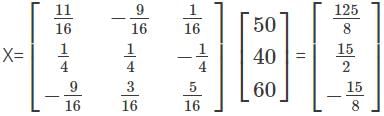


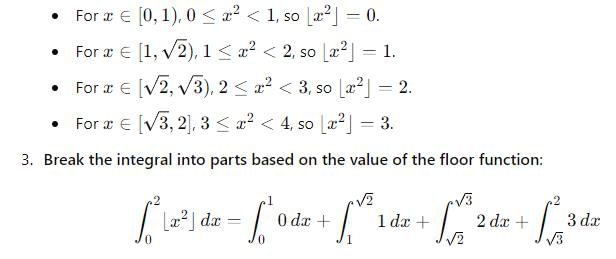

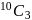 .
.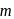 arked '-' out of eight places
arked '-' out of eight places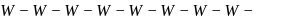
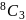 ways
ways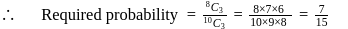

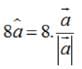
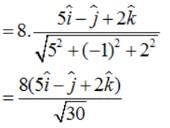
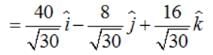
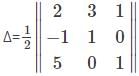
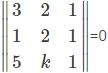
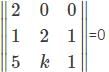
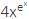 with respect to x.
with respect to x.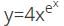

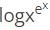 (∵logab =loga+logb)
(∵logab =loga+logb)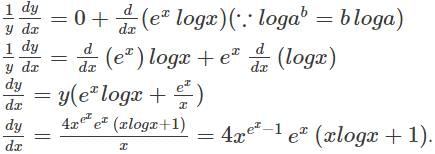
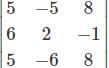
 = 40-40 = 0
= 40-40 = 0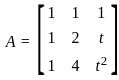 is invertible, we can analyze its determinant. A matrix is invertible if and only if its determinant is nonzero.
is invertible, we can analyze its determinant. A matrix is invertible if and only if its determinant is nonzero.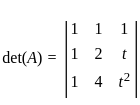
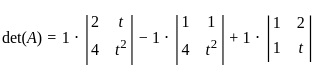
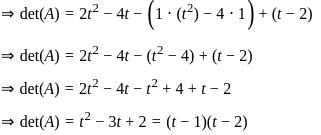

 is
is
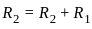

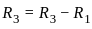
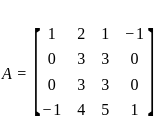
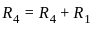
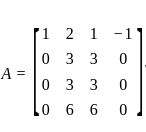
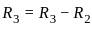
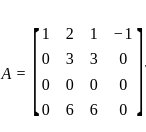
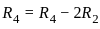
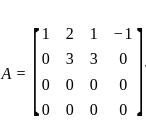
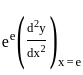 is:
is: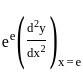 = 4 -1/e
= 4 -1/e










