All Courses
Get the App Signup / Login
Sign in Open App
JEE Exam  >  JEE Tests  >  Matrix And Determinants MCQ (With Solution) -2 (Competition Level 1) - JEE MCQ

Matrix And Determinants MCQ (With Solution) -2 (Competition Level 1) - JEE MCQ


Test Description

20 Questions MCQ Test - Matrix And Determinants MCQ (With Solution) -2 (Competition Level 1)

Matrix And Determinants MCQ (With Solution) -2 (Competition Level 1) for JEE 2024 is part of JEE preparation. The Matrix And Determinants MCQ (With Solution) -2 (Competition Level 1) questions and answers have been prepared according to the JEE exam syllabus.The Matrix And Determinants MCQ (With Solution) -2 (Competition Level 1) MCQs are made for JEE 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Matrix And Determinants MCQ (With Solution) -2 (Competition Level 1) below.
Solutions of Matrix And Determinants MCQ (With Solution) -2 (Competition Level 1) questions in English are available as part of our course for JEE & Matrix And Determinants MCQ (With Solution) -2 (Competition Level 1) solutions in Hindi for JEE course. Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free. Attempt Matrix And Determinants MCQ (With Solution) -2 (Competition Level 1) | 20 questions in 60 minutes | Mock test for JEE preparation | Free important questions MCQ to study for JEE Exam | Download free PDF with solutions
Matrix And Determinants MCQ (With Solution) -2 (Competition Level 1) - Question 1
Save

Detailed Solution for Matrix And Determinants MCQ (With Solution) -2 (Competition Level 1) - Question 1

Applying R1 → R1+ R3 to obtain

As 0 < sin2 θ < 1, we get Δ ∈ [2, 4]

Matrix And Determinants MCQ (With Solution) -2 (Competition Level 1) - Question 2
Save

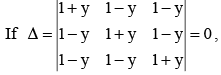then value of y are 

Detailed Solution for Matrix And Determinants MCQ (With Solution) -2 (Competition Level 1) - Question 2

Using C1 → C1 + C2 + C3 , we get
 R3 → R3 - R2 , R2 → R2 - R1 we get
 

1 Crore+ students have signed up on EduRev. Have you? Download the App
Matrix And Determinants MCQ (With Solution) -2 (Competition Level 1) - Question 3
Save

Let f (n) = an+ bn and 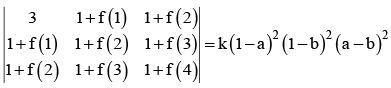, then k =

Detailed Solution for Matrix And Determinants MCQ (With Solution) -2 (Competition Level 1) - Question 3





Matrix And Determinants MCQ (With Solution) -2 (Competition Level 1) - Question 4
Save

If the value of a third order determinant is 11, then the value of the square of the determinant formed by its cofactors will be
Detailed Solution for Matrix And Determinants MCQ (With Solution) -2 (Competition Level 1) - Question 4

Matrix And Determinants MCQ (With Solution) -2 (Competition Level 1) - Question 5
Save

If a, b, c are non-zero real numbers then the value of 
Detailed Solution for Matrix And Determinants MCQ (With Solution) -2 (Competition Level 1) - Question 5



Matrix And Determinants MCQ (With Solution) -2 (Competition Level 1) - Question 6
Save

 then, the value of
Detailed Solution for Matrix And Determinants MCQ (With Solution) -2 (Competition Level 1) - Question 6

Matrix And Determinants MCQ (With Solution) -2 (Competition Level 1) - Question 7
Save

then the real value of x is
Detailed Solution for Matrix And Determinants MCQ (With Solution) -2 (Competition Level 1) - Question 7



Matrix And Determinants MCQ (With Solution) -2 (Competition Level 1) - Question 8
Save

Detailed Solution for Matrix And Determinants MCQ (With Solution) -2 (Competition Level 1) - Question 8

Degree of LHS = Degree of RHS
n + (n + 2) + (n + 4) = (-2) + (-2) + (-2)
3n + 6 = -6
3n =-12
n =-4

Matrix And Determinants MCQ (With Solution) -2 (Competition Level 1) - Question 9
Save

Let a, b, c be such that b(a + c) ≠ 0. If 

then the value of n is:
Detailed Solution for Matrix And Determinants MCQ (With Solution) -2 (Competition Level 1) - Question 9



Matrix And Determinants MCQ (With Solution) -2 (Competition Level 1) - Question 10
Save

Detailed Solution for Matrix And Determinants MCQ (With Solution) -2 (Competition Level 1) - Question 10

Skew symmetric determinant of order = 3

Matrix And Determinants MCQ (With Solution) -2 (Competition Level 1) - Question 11
Save

If a, b, c, d > 0, x∈R and (a2 + b2 + c2) x2 - 2 (ab + bc + cd ) x + b2 + c2 + d2 < 0 then, 
Detailed Solution for Matrix And Determinants MCQ (With Solution) -2 (Competition Level 1) - Question 11


 (a, b, c, d are in G.P, log a, logb, logc are in A.P) 

Matrix And Determinants MCQ (With Solution) -2 (Competition Level 1) - Question 12
Save

Detailed Solution for Matrix And Determinants MCQ (With Solution) -2 (Competition Level 1) - Question 12

Matrix And Determinants MCQ (With Solution) -2 (Competition Level 1) - Question 13
Save

Choose any 9 distinct integers. These 9 integers can be arranged to form 9! Determinants each of order 3. Then sum of these 9! Determinants is
Detailed Solution for Matrix And Determinants MCQ (With Solution) -2 (Competition Level 1) - Question 13

For any Δ, then exist -Δ in arrangements
∴ sum = 0

Matrix And Determinants MCQ (With Solution) -2 (Competition Level 1) - Question 14
Save

The determinant 
Detailed Solution for Matrix And Determinants MCQ (With Solution) -2 (Competition Level 1) - Question 14


= -p(xp - z) (xz - y2) = 0 ⇒ x, y, z are in G.P.

Matrix And Determinants MCQ (With Solution) -2 (Competition Level 1) - Question 15
Save

The parameter on which the value of the determiant

 does not depend upon, is
Detailed Solution for Matrix And Determinants MCQ (With Solution) -2 (Competition Level 1) - Question 15


sin (dx) - a sin (2dx) + a2 sin (dx)
Is independent of p

Matrix And Determinants MCQ (With Solution) -2 (Competition Level 1) - Question 16
Save

Detailed Solution for Matrix And Determinants MCQ (With Solution) -2 (Competition Level 1) - Question 16

Applying R1 → R1+ R3 to obtain

Matrix And Determinants MCQ (With Solution) -2 (Competition Level 1) - Question 17
Save

If   then value of y are 
Detailed Solution for Matrix And Determinants MCQ (With Solution) -2 (Competition Level 1) - Question 17

Using C1 → C1 + C2 + C3 , we get 

Matrix And Determinants MCQ (With Solution) -2 (Competition Level 1) - Question 18
Save

Find the value of the determinant  where a, b and c are respectively the pth, qth and rth terms of a harmonic progression  
Detailed Solution for Matrix And Determinants MCQ (With Solution) -2 (Competition Level 1) - Question 18





Matrix And Determinants MCQ (With Solution) -2 (Competition Level 1) - Question 19
Save

Type of matrix determinant in which value of one element contained in matrix is classified as determinant of
Matrix And Determinants MCQ (With Solution) -2 (Competition Level 1) - Question 20
Save

Detailed Solution for Matrix And Determinants MCQ (With Solution) -2 (Competition Level 1) - Question 20
First do C1-C2, and C2-C3 then take out common (a-b) from C1 and (b-c) from C1 and solve again the remaining matrix ,we get option A
Information about Matrix And Determinants MCQ (With Solution) -2 (Competition Level 1) Page
In this test you can find the Exam questions for Matrix And Determinants MCQ (With Solution) -2 (Competition Level 1) solved & explained in the simplest way possible. Besides giving Questions and answers for Matrix And Determinants MCQ (With Solution) -2 (Competition Level 1), EduRev gives you an ample number of Online tests for practice

Top Courses for JEE

Download as PDF

Top Courses for JEE

Important Questions for Matrix And Determinants MCQ (With Solution) -2 (Competition Level 1)

Find all the important questions for Matrix And Determinants MCQ (With Solution) -2 (Competition Level 1) at EduRev.Get fully prepared for Matrix And Determinants MCQ (With Solution) -2 (Competition Level 1) with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the Matrix And Determinants MCQ (With Solution) -2 (Competition Level 1) syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of Matrix And Determinants MCQ (With Solution) -2 (Competition Level 1) resources.

Matrix And Determinants MCQ (With Solution) -2 (Competition Level 1)

Prepare for the Matrix And Determinants MCQ (With Solution) -2 (Competition Level 1) within the JEE exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for Matrix And Determinants MCQ (With Solution) -2 (Competition Level 1)

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace Matrix And Determinants MCQ (With Solution) -2 (Competition Level 1) with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Follow Us
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup