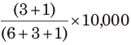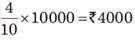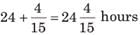Miscellaneous Test: Time & Work- 2 - Bank Exams MCQ
25 Questions MCQ Test - Miscellaneous Test: Time & Work- 2
X Can finish a piece of work in 12 days while Y can do it in 15 days. If both work at it together. How much time will they take to do the work?
X can do piece of work in 5 days. Y can do it in 10 days. With the help of Z, they finish the work in 2 days. In how many days Z alone can do the whole work?
A is thrice as good a work man as B and takes 10 days less to do a piece of work than B takes. The number of days taken by B to finish the work is:
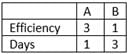
Ajit is 3 times as efficient as Bablu, then the ratio of number of days required by each to work alone, completely?
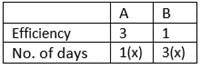
A is thrice as efficient as B. Working together they complete the work in 3 days. If B takes 8 days more than A, what is the number of days taken by A to finish the whole work, alone?
Ganga, Jamuna and Saraswati can do a piece of work, working together, in 1 day. Ganga is thrice efficient as Jamuna and Jamuna takes the twice the number of days as Saraswati takes to do it alone. What is the difference between the number of days taken by Ganga and Saraswati?
A and B can complete a task in 30 days when working together. After A and B have been working together for 11 days, B is called away and A, all by himself completes the task in the next 28 days. Had A been working alone from begining, the number of days taken by him to complete the task would have been:
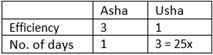
Efficiency of Asha is 25% more than Usha and Usha takes 25 days to complete a piece of work, Asha started a work alone and then Usha joined her 5 days before actual completion of the work. For how many days Asha worked alone?
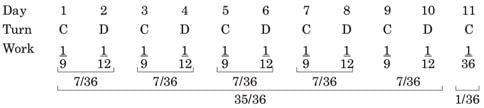
Chandni and Divakar can do a piece of work in 9 days and 12 days respectively. If they work for a day alternatively, Chandni beginning, in how many days, the work will be completed?
A group of men decided to do a job in 4 days. 20 men dropped out from the task every day due to which work was completed in 7 days. How many men were there at the beginning?
The number of days required by A,B and C to work individually is 6, 12 and 8 respectively. They started a work doing it alternatively. If A has started then followed by B and so on, how many days are needed to complete the whole work?
When A,B and C are deployed for a task, A and B together do 70% of the work and B and C together do 50% of the work. Who is most efficient?
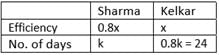
Sharma is 20% less efficient than Kelkar. If Kelkar can do a piece of work in 24 days. the number of days required by Sharma to complete the same work alone will be—
If 10 persons can do a job in 20 days, then 20 person with twice the efficiency can do the same job in:
30 workers can finish a work in 20 days. After how many days should 9 workers leave the job so that the work is completed in total 26 days :
Mr. Modi can copy 40 pages in 10 minutes, Mr. Xerox and Mr. Modi both working together can copy 250 in 25 minutes. In how many minutes Mr. Xerox can copy 36 pages?
6 children and 2 men complete a certain piece of work in 6 days. Each child takes twice the time taken by a man to finish the work. In how many days will 5 men finish the same work?
Directions for question : A can do a work in 15 days and B can do it in 18 days. with the help of C work is completed in 6 days.
Q. How long will it take for C to finish the work alone?
Directions for question : A can do a work in 15 days and B can do it in 18 days. with the help of C work is completed in 6 days.
Q. A,B and C received total ₹ 27,000 for the whole work. What is the share of B, if the money is distributed in the ratio of amount of work done, individually?
314 weavers weaves 6594 shawls in 1 / 6 hours. What is the number of shawls weaved per hour by an average weaver?
If 20 engineers and 20 workers can together construct a 20 km road in 20 days. 40 engineers and 40 workers together will construct 40 km road in how many days?
A man, a woman and a girl worked for a contractor for the same period. A man is twice efficient as a woman and a woman is thrice efficient as a girl. ₹ 10000 were given to all of them. What is the sum of money received by a woman and a girl together?
There was a leakage in the container of the refined oil. If 11 kg oil leaks out per day then it would have lasted for 50 days, if the leakage was 15 kg per day, then it would have lasted for only 45 days. For how many days would the oil have lasted, if there was no leakage and it was completely used for eating purpose?
Tap A can fill a tank in 20 hours, B in 25 hours but tap C can empty a full tank in 30 hours. Starting with A, followed by B and C each tap opens alternatively for one hour period till the tank gets filled up completely. In how many hours the tank will be filled up completely?
Pipe A can fill the tank in 4 hours, while pipe B can fill it in 6 hours working separately. Pipe C can empty the whole tank in 4 hours. Ramesh opened the pipe A and B simultaneously to fill the empty tank. He wanted to adjust his alarm so that he could open the pipe C when it was half-filled, but he mistakenly adjusted his alarm at a time when his tank would be 3/4th filled. What is the time difference between both the cases, to fill the tank fully.





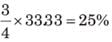
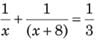


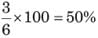
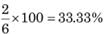
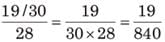
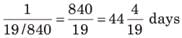
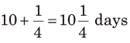
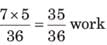
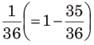 work will be done by Chandni =
work will be done by Chandni = 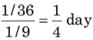
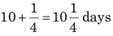

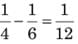
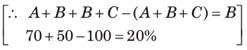
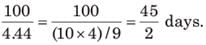
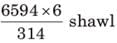 = 126 shawls
= 126 shawls