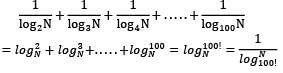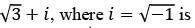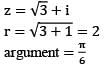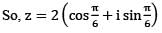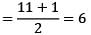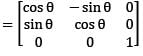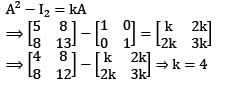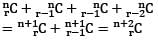NDA I - Mathematics Question Paper 2018 - Defence MCQ
30 Questions MCQ Test - NDA I - Mathematics Question Paper 2018
If n ∈ N, then 121n - 25n 1900n − (−4)n is divisible by which of the following?
In the expansion of (1 + x)43, if the coefficients of (2r + 1)th and (r + 2)th terms are equal, then what is the value of r(r ≠ 1)?
What is the principal argument of (−1 − i), where 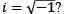
Let α and β be real numbers and z be a complex number. If z2 + αz + β = 0 has two distinct non-real roots with real roots Re(z) = 1, then it is necessary that
Let A and B be subsets of X and C = (A ∩ B′) ∪ (A′ ∩ B), where A’ and B’ are complements of A and B respectively in X. What is C equal to?
How many numbers between 100 and 1000 can be formed with the digits 5, 6, 7, 8, 9 if the r epetition of digits is not allowed?
The number of non-zero integral solutions of the equation |1 − 2i|x = 5x is
If the ratio of AM to GM of two positive numbers a and b is 5:3, then a:b is equal to
If coefficients of am and an in the expansion of (1 + a)m+n are α and β, then which one of the following is correct?
If x + log15(1 + 3x) = x log155 + log1512, where x is an integer, then what is x equal to?
How many four-digit numbers divisible by 10 can be formed using 1, 5, 0, 6, 7 without repetition of digits?
In a class, 54 students are good in Hindi only, 63 students are good in Mathematics only, and 41 students are good in English only. There are 18 students who are good in both Hindi and Mathematics. 10 students are good in all three subjects.
Q. What is the number of students who are good in either Hindi or Mathematics but not in English?
In a class, 54 students are good in Hindi only, 63 students are good in Mathematics only, and 41 students are good in English only. There are 18 students who are good in both Hindi and Mathematics. 10 students are good in all three subjects.
Q. What is the number of students who are good in Hindi and Mathematics but not in English?
If α and β are different complex numbers with |α| = 1, then what is 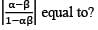
The binary number expression of the decimal number 31 is
What is i1000 + i1001 + i1002 + i1003 equal to 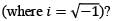
What is the number of non-zero terms in the expansion of 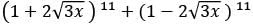 (after simplification)?
(after simplification)?
What is the greatest integer among the following by which the number 55 + 75 is divisible?
If x = 1 − y + y2 − y3 + … up to infinite terms, where |y| < 1, then which one of the following is correct?
If A is a 2 × 3 matrix and AB is a 2 × 5 matrix, then B must be a
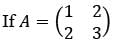 and A2 − kA − I2 = O, where I2 is the 2 × 2 identity matrix, then what is the value of k?
and A2 − kA − I2 = O, where I2 is the 2 × 2 identity matrix, then what is the value of k?
What is the number of triangles that can be formed by choosing the vertices from a set of 12 points in a plane, seven of which lie on the same straight line?
What is C(n, r) + 2C (n, r − 1) + C(n, r) equal to?
Let [x] denote the greatest integer function. What is the number of solutions of the equation x2 + 4x + [x] = 0 in the interval [0,2]?
A survey of 850 students in a University yields that 680 students like music and 215 like dance. What is the least number of students who like both music and dance?


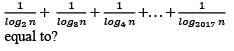
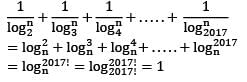

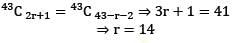
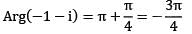
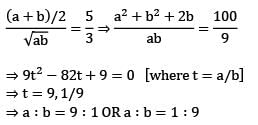
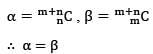
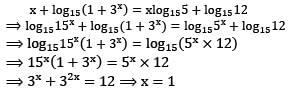
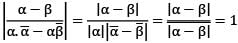
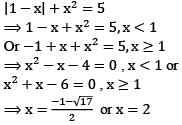
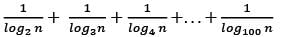 equal to (n ≠ 1)?
equal to (n ≠ 1)?