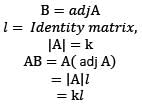NDA II - Mathematics Question Paper 2018 - NDA MCQ
30 Questions MCQ Test - NDA II - Mathematics Question Paper 2018
If an infinite GP has the first term x and the sum 5, then which of the following is correct?
Consider the following expressions:
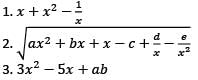
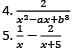
Which of the above are rational expressions?
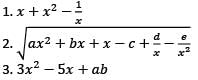
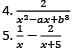
Which of the above are rational expressions?
A square matrix A is called orthogonal if
Where A’ is the transpose of A.
If A, B and C are subsets of a Universal set, then which one of the following is not correct?
Where A’ is the complement of A.
Let x be the number of integers lying between 2999 and 8001 which have at least two digits equal. Then x is equal to
A survey was conducted among 300 students. If was found that 125 students like to play cricket, 145 students like to play football and 90 students like to play tennis. 32 students like to play exactly two games out of the three games.
Q. How many students like to play all the three games?
How many students like to play exactly only one game?
If α and β(≠ 0) are the roots of the quadratic Equation x2 + αx − β = 0, then the quadratic expression −x2 + αx + β = 0, where x ∈ R has
What is the coefficient of the middle term in the binomial expansion of (2+3x)4?
For a square matrix A, which of the following
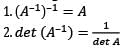
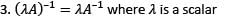
Select the correct answer using the code given below:
Which one of the following factors does the expansions of the determinant
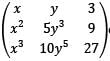 contain?
contain?
There are 17 cricket players, out of which 5 players can bowl. In how many ways can a team of 11 players be selected so as to include 3 bowlers?
If A and B are two invertible square matrices of same order, then what is (AB)−1 equal to?
If a + b + c = 0, then one of the solutions of
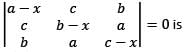
What should be the value of x so that the matrix 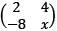 does not have an inverse?
does not have an inverse?
The system of equations
2x + y – 3z = 5
3x – 2y + 2z = 5 and
5x – 3y – z = 16
Which one of the following is correct in respect of the cube roots of unity?
If u, v and w (all positive) are the  terms of a GP, the determinant of the matrix
terms of a GP, the determinant of the matrix
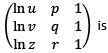
Let the coefficient of the middle term of the binomial expansion of (1 + x)2n be α and those of two middle terms of the binomial expansion of (1 + x)2n– 1 be β and γ . Which one of the following relations is correct?
Let 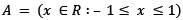
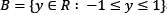 and S be the subset of A × B, defined by
and S be the subset of A × B, defined by 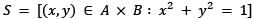 Which one of the following is correct?
Which one of the following is correct?
Let Tr be the rtℎ term of an AP for r = 1, 2, 3,…… If for some distinct positive integers m and n we have 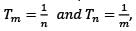 then what is Tmn equal to?
then what is Tmn equal to?
Suppose f(x) is such a quadratic expression that it is positive for all real x. If 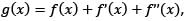 then for any real x. Then for any real x.
then for any real x. Then for any real x.
Consider the following in respect of matrices A, B and C of same order:
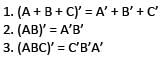
Where A’ is the transpose of the matrix A. Which of the above are correct?
The sum of the binary numbers (11011)2 , (10110110)2 and (10011x0y)2 is the binary number (101101101)2 . What are the values of x and y?
Let matrix B be the adjoint of a square matrix A, l be the identity matrix of same order as A. If k(≠ 0) is the determinant of the matrix A, then what is AB equal to?


 equal to?
equal to?
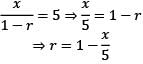
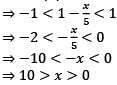

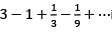 is equal to
is equal to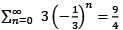
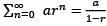
 we can apply the formula to obtain
we can apply the formula to obtain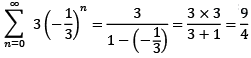
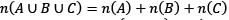
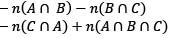
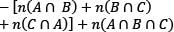
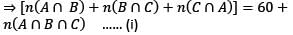
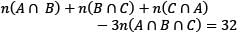
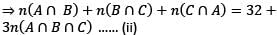
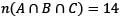
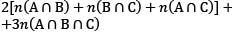
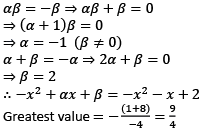
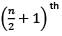 term is the middle term.
term is the middle term.
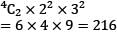
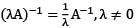
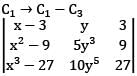
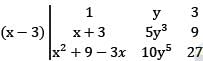
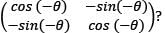
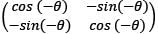
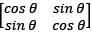
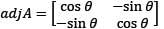
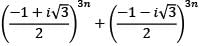
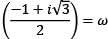
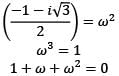
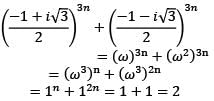
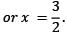
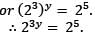
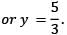
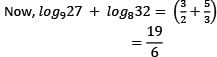

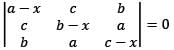
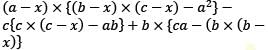
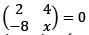
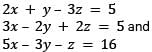

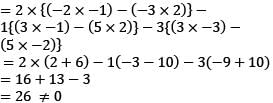
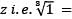 z.
z.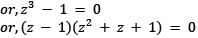
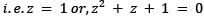
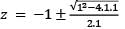
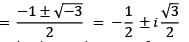
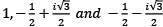 among them 1 is real number and the other two are conjugate complex numbers and they are also known as imaginary cube roots of unity.
among them 1 is real number and the other two are conjugate complex numbers and they are also known as imaginary cube roots of unity.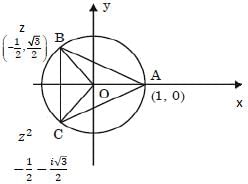
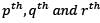 terms of a GP whose first term is A and common ratio is R
terms of a GP whose first term is A and common ratio is R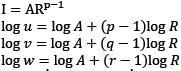
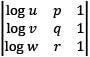
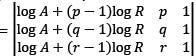
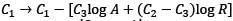
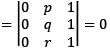
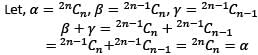
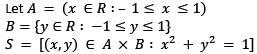
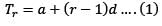
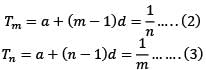
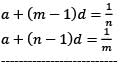
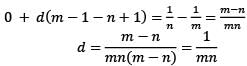
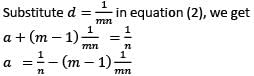
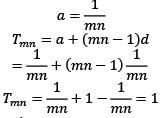
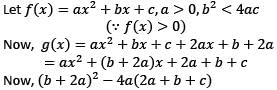
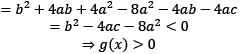
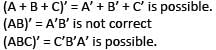

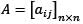 is an identity matrix, if
is an identity matrix, if 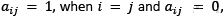 when i ≠ j
when i ≠ j