NDA Mock Test: Mathematics - 10 - NDA MCQ
30 Questions MCQ Test NDA (National Defence Academy) Mock Test Series 2025 - NDA Mock Test: Mathematics - 10
A man covers a certain distance at a certain speed. Had he moved 6 km / h faster, he would have taken 4 hours less. If he had moved 8 km / h slower, he would have taken 10 hours more. How much time (in hours) will he take to cover the same distance with his usual speed?
A train starts at 3:00 pm from Mumbai and moves towards Ahmedabad at the speed of 20 km/hr. Another train starts from Ahmedabad at 8 pm and moves towards Mumbai at the speed of 60 km/hr. If the distance between Mumbai and Ahmedabad is 600 km, then at what time both the trains will meet?
A shopkeeper offers 2 schemes of discounts. First scheme is series of discounts of 10% and 20%. Second scheme is series of discounts of 15% and 15%. Which scheme gives more discount and by how much?
Find the number of LED TVs produced by the brand Bb in 2020.
Determine the nature of the roots of the equation 2x2 + 5x + 5 = 0
Find the area of the sector of third circle whose angle is 60°.
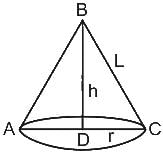
The area of the circular base of the tent house is 308 m2, and its height is 7√2 m. Then find the area (in m2) of cloth required to cover the curved surface area of the conical tent.
Gagan has a total of 30 marbles, out of which 18 are red and 12 are blue. Jane has a total of 20 marbles, all of which are red or blue. If the ratio of red to blue marbles is the same for both Gagan and Jane, then how many more blue marbles does Gagan have than Jane?
The two regression coefficients byx and bxy respectively are
What is a1 + a5 - a10 - a15 - a20 - a25 + a30 + a34 equal to ?
The table given below shows the income and expenditure of five companies.
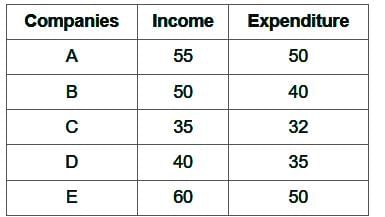
What is the difference between average income and average expenditure of all the companies?
|
2 docs|101 tests
|



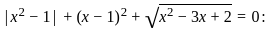
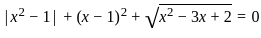
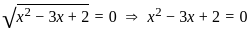
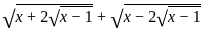 ?
?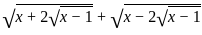
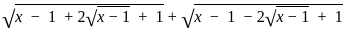
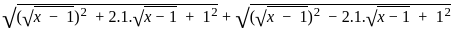
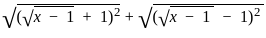
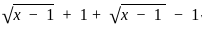
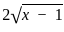
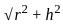
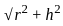
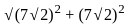
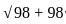
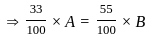
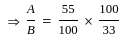
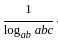 +
+ 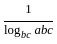 +
+ 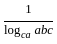 =
= 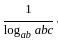 +
+ 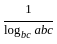 +
+ 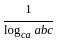
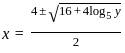
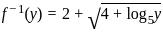
 .
.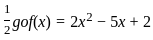 , then f(x) is equal to
, then f(x) is equal to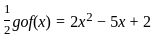
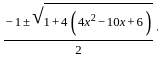
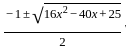
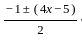 = 2x - 3, -2x + 2
= 2x - 3, -2x + 2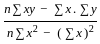

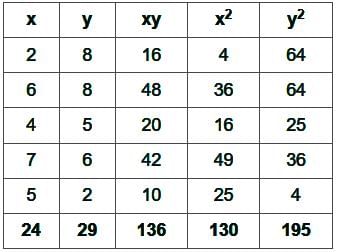
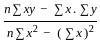
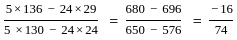 = -0.216
= -0.216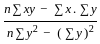
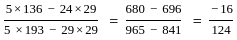 = -0.129
= -0.129















