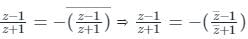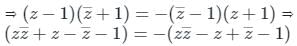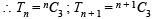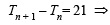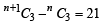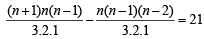NDA Mock Test: Mathematics - 6 - NDA MCQ
30 Questions MCQ Test NDA (National Defence Academy) Mock Test Series 2025 - NDA Mock Test: Mathematics - 6
Two sets, A and B, are as under:
A = {(a, b) ∈ R × R : |a − 5| < 1 and |b − 5| < 1};
B = {a, b) ∈ R × R : 4 (a − 6)2 + 9(b−5) 2 ≤ 36}. Then,
A = {(a, b) ∈ R × R : |a − 5| < 1 and |b − 5| < 1};
B = {a, b) ∈ R × R : 4 (a − 6)2 + 9(b−5) 2 ≤ 36}. Then,
Consider the following statements:
1. If (a + b) is directly proportional to (a - b), then (a2 + b2) is is directly proportional to ab.
2. If a is directly proportional to b, then (a2 - b2) is directly proportional to ab.
Which of the statements given above is/are correct?
Consider the following statements:
1. One of the roots of the equation is always less than 1 if a, b and c are all positive.
2. One of the roots of the equation is always negative if a, b and c are all negative.
Which of the statements given above is/are correct?
1. One of the roots of the equation is always less than 1 if a, b and c are all positive.
2. One of the roots of the equation is always negative if a, b and c are all negative.
Which of the statements given above is/are correct?
Consider the following statements:
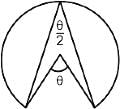
1. The angle in a sector greater than a semicircle is less than a right angle.
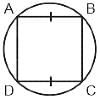
2. If two sides of a pair of opposite sides of a cyclic quadrilateral are equal, then its diagonals are also equal.
Which of the statements given above is/are correct?
Consider the following statements :
1. The age of F cannot be determined due to insufficient data.
2. The average weight of D and F is equal to weight of E.
3. The weight difference is maximum for D and A.
Which of the statements given above are correct?
Question: Is m > n if m, n are real numbers?
Statement-I:
m = (1 - p) (p2 + p + 1) and
n = (p + 1) (p2 - p + 1)
Statement-II:
m = pn
Question: What is the other root of the quadratic equation with real coefficients if one of the roots is 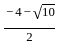 ?
?
Statement-I: The product of the roots is 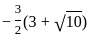
Statement-II: The sum of roots of quadratic equation is -1.
Question: What is the 3-digit number which is divisible by 10?
Statement-I: If the digits in hundred's place and ten's place of the number are interchanged, the resulting number is diminished by 180.
Statement-II: If the digit in hundred's place is halved and digit in ten's place and unit place of the number are interchanged, the resulting number is diminished by 336.
Question: Are x, y, z equal, where x, y, z are real numbers?
Statement-I: x2 + y2 + z2 - xy - yz - zx = 0
Statement-II: x3 + y3 + z3 - 3xyz = 0
Question: What is the ratio x ∶ y ∶ z equal to if x, y, z ≠ 0?
Statement-I: x + z/y = z/x
Statement-II: z - y/x = x/z
Question: What is the sum of two natural numbers?
Statement-I: LCM of the two numbers is 144.
Statement-II: One of the numbers is 72.
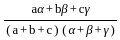 equal to ?
equal to ?
If (x - 1)3 is a factor of x4 + αx3 + βx2 + γx - 1, then the other factor will be:
A 2-digit number is such that the sum of the number and the number obtained by reversing the order of the digits of the number is 55. Further, the difference of the given number and the number obtained by reversing the order of the digits of the number is 45. What is the product of the digits?
A person borrowed Rs. 10,000 at 12% rate of interest per annum compounded quarterly for a period of 9 months. What is the interest paid by him to settle his account after 9 months?
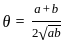 possible?
possible?
If A = {2, 3, 4, 8, 10}, B = {3, 4, 5, 10, 12}, C = {4, 5, 6, 12, 14} then (A ∩ B) ∪ (A ∩ C) is equal to:
If f(x) = x – x2, then f(a + 1) – f(a – 1) , a ∈ R is :
The minor Mij of an element aij of a determinant is defined as the value of the determinant obtained after deleting the
If z is a complex number such that 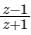 is purely imaginary, then what is |z| equal to ?
is purely imaginary, then what is |z| equal to ?
Let Tn denote the number of triangles which can be formed using the vertices of a regular polygon of n sides. If Tn + 1 - Tn = 21, then n equals (2001S)
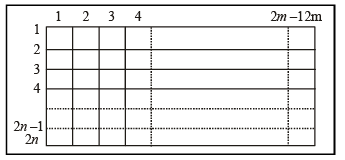
A rectangle with sides of length (2m – 1) an d (2n – 1) units is divided into squares of unit length by drawing parallel lines as shown in the diagram, then the number of rectangles possible with odd side length s is (2005S)

In how many ways, a party of 5 men and 5 women be seated at a circular table, so that no two women are adjacent?
In how many ways can 4 red, 3 yellow and 2 green chairs be arranged in a row if the chairs of the same colour are indistinguishable?
|
2 docs|101 tests
|


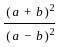
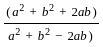 =
= 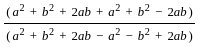
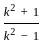
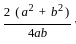
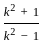
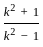 (2ab)
(2ab) 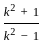 & 2 is constant.
& 2 is constant.

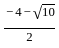
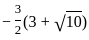
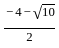
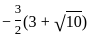
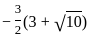 ×
× 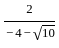
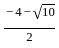
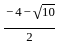 )
)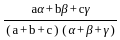 =
= 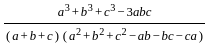
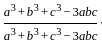 = 1
= 1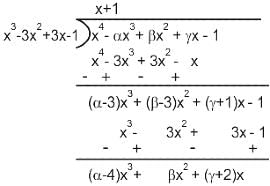
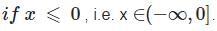
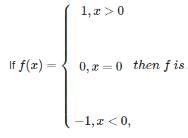
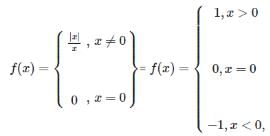
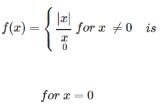

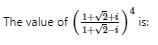
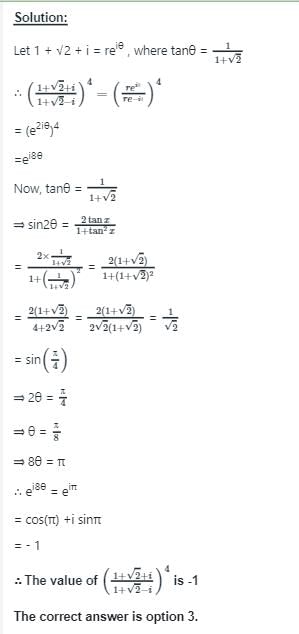
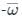
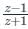 is purely imaginary,
is purely imaginary, = a + ib, then a = 0
= a + ib, then a = 0