NDA Mock Test: Mathematics - 8 - NDA MCQ
30 Questions MCQ Test NDA (National Defence Academy) Mock Test Series 2025 - NDA Mock Test: Mathematics - 8
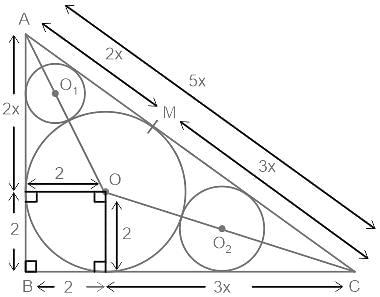
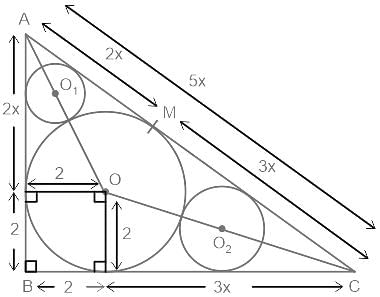
What is the radius of the circle with centre at O1?
Statement I: The product of r consecutive number is divisible by r!
Statement II: The product of r consecutive number is divisible by (r + 1)!
For what value of k, is the polynomial f(x) = 3x4 - 9x3 + x2 + 15x + k completely divisible by 3x2 - 5?
Which of the following statement is/are true?
A) Unit digit of 12345 × 54456 + 78698 is 4
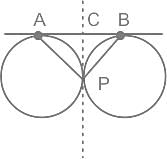
B) Unit digit of 125! is 5Two circles touch each other externally at points P and AB is a direct common tangent which touches the circles at A and B, respectively. ∠APB is:
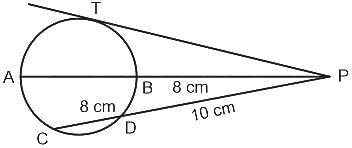
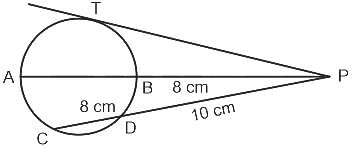
In the given figure, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. If CD = 8 cm, PD = 10 cm and PB = 8 cm, find AB.
The total surface of a solid right circular cylinder is 372 π cm2, and its height is 25 cm. Its volume is equal to 1/5 of the volume of a sphere. The surface area (in cm2) of the sphere is:
What is the area of the equilateral triangle, if the perimeter of the equilateral triangle is equal to the circumference of the circle whose radius is (OA + 16) cm?
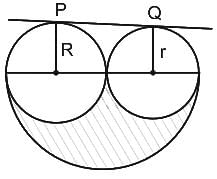
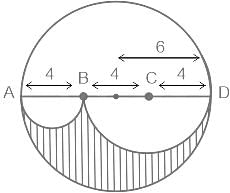
In the given figure , find the area of the shaded region, if the length of direct common tangent is 16 cm.
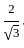 , then what is (tan α + cot α) equal to?
, then what is (tan α + cot α) equal to?
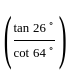
In 't' years, the simple interest earned on a certain amount at the rate of 10% per annum is 5/8th of the principal amount. If the rate of interest is made three-fourth of 10% and the simple interest remains the same, which of the following statements is true about the changed value of time?
Akash is thrice as good a workman as Arvind and therefore is able to finish a job in 30 days less than Arvind. If they work together, in how many days can they finish the job?
A and B are working on an assignment. A takes 6 hours to type 32 pages on a computer while B takes 5 hours to type 40 pages. How much time will they take, working together on two different computers, to type an assignment of 110 pages?
Study the given table and answer the question that follows.
The data given in the table is for the month of December 2022.
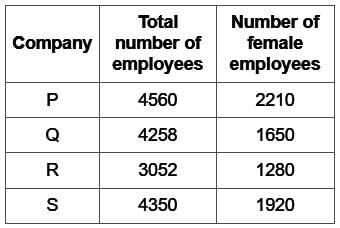
What is the difference between the number of male employees in company P and that in company R?
|
2 docs|101 tests
|


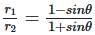
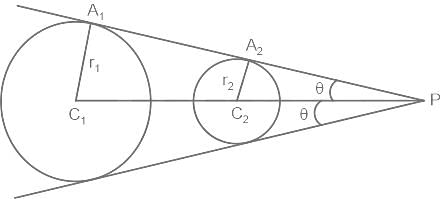
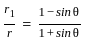
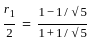
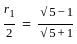
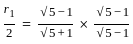
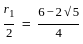

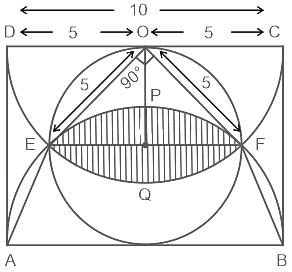
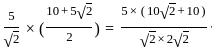
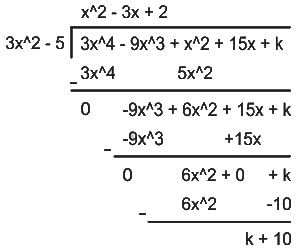
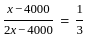
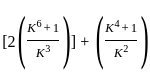 ?
?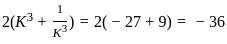
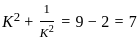
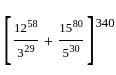 :
: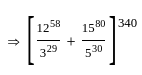
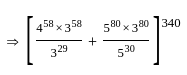
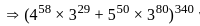
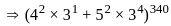

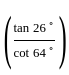
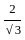 ,
,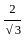
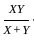 days.
days.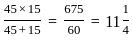 days.
days.










