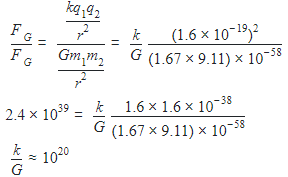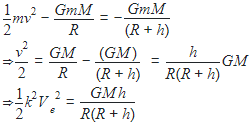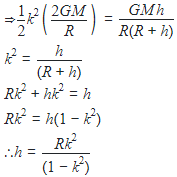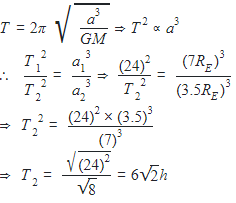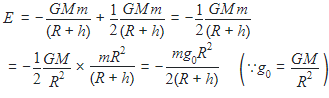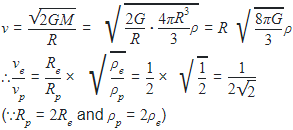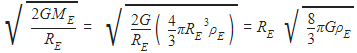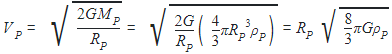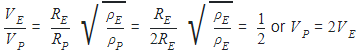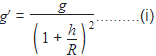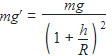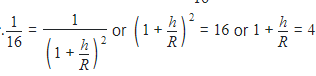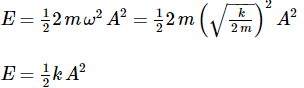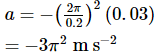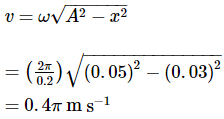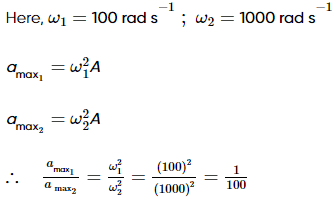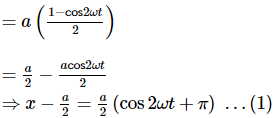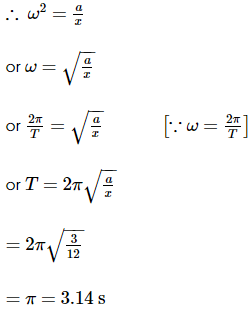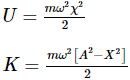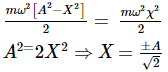All Courses
Get the App Signup / Login
Sign in Open App
NEET Exam  >  NEET Tests  >  NEET Mock Test Series 2025  >  NEET Minor Test - 4 - NEET MCQ

NEET Minor Test - 4 - NEET MCQ


Test Description

30 Questions MCQ Test NEET Mock Test Series 2025 - NEET Minor Test - 4

NEET Minor Test - 4 for NEET 2024 is part of NEET Mock Test Series 2025 preparation. The NEET Minor Test - 4 questions and answers have been prepared according to the NEET exam syllabus.The NEET Minor Test - 4 MCQs are made for NEET 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for NEET Minor Test - 4 below.
Solutions of NEET Minor Test - 4 questions in English are available as part of our NEET Mock Test Series 2025 for NEET & NEET Minor Test - 4 solutions in Hindi for NEET Mock Test Series 2025 course. Download more important topics, notes, lectures and mock test series for NEET Exam by signing up for free. Attempt NEET Minor Test - 4 | 180 questions in 200 minutes | Mock test for NEET preparation | Free important questions MCQ to study NEET Mock Test Series 2025 for NEET Exam | Download free PDF with solutions
NEET Minor Test - 4 - Question 1
Save

A body of mass 60g experiences a gravitational force of 3.0N, when placed at a particular point. The magnitude of the gravitational field intensity at that point is

Detailed Solution for NEET Minor Test - 4 - Question 1

F = mEG

3 = 60/1000 EG

EG = 50N / kg

NEET Minor Test - 4 - Question 2
Save

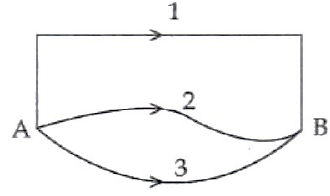
A gravitational field is present in a region and a mass is shifted from A to B through different paths as shown. If W1 W2 and W3 represent the work done by the gravitational force along the respective paths, then:

Detailed Solution for NEET Minor Test - 4 - Question 2
Gravitational force is a conservative force work done by conservative force is path independent.

Hence, ∴ W1 = W2 = W3

1 Crore+ students have signed up on EduRev. Have you? Download the App
NEET Minor Test - 4 - Question 3
Save

The ratio of Coulomb's electrostatic force to the gravitational force between an electron and a proton separated by some distance is 2.4 × 1039. The ratio of the proportionality constant, to the Gravitational constant G is nearly (Given that the charge of the proton and electron each =1.6 × 10−19C, the mass of the electron = 9.11 × 10−31kg, the mass of the proton = 1.67×10−27kg ) :

Detailed Solution for NEET Minor Test - 4 - Question 3

NEET Minor Test - 4 - Question 4
Save

A particle of mass ' m ' is projected with a velocity v = kVe (k < 1) from the surface of the earth. (Ve = escape velocity) The maximum height above the surface reached by the particle is
Detailed Solution for NEET Minor Test - 4 - Question 4
given v=kVe

where, k < />

Thus, v < />e

From conservation of mechanical energy,

We know,

NEET Minor Test - 4 - Question 5
Save

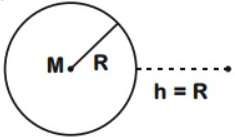
The work done to raise a mass m from the surface of the earth to a height h, which is equal to the radius of the earth, is
Detailed Solution for NEET Minor Test - 4 - Question 5
Initial potential energy at earths surface is Ui = −GMm/R

Final potential energy at height h = R

As work done = change in PE

∴ W = Uf − Ui

= GMm /

(∵ GM = gR2)

=

NEET Minor Test - 4 - Question 6
Save

The time period of a geostationary satellite is 24h, at a height 6RE(RE. is radius of earth) from surface of earth. The time period of another satellite whose height is 2.5RE from surface will be,(
Detailed Solution for NEET Minor Test - 4 - Question 6

NEET Minor Test - 4 - Question 7
Save

If the mass of the Sun were ten times smaller and the universal gravitational constant were ten times larger in magnitude, which of the following is not correct?
Detailed Solution for NEET Minor Test - 4 - Question 7
′g′ on the earth will not change.

If universal gravitational constant become term then G′ = 10G

Acceleration due to gravity, ,g = Gm/R2

So, Acceleration due to gravity increases.

NEET Minor Test - 4 - Question 8
Save

Two astronauts are floating in gravitational free space after having lost contact with their spaceship. The two will
Detailed Solution for NEET Minor Test - 4 - Question 8
Since two astronauts are floating in gravitational free space. The only force acting on the two astronauts is the gravitational pull of their masses,

F = Gm1m2,

which is attractive in nature.

Hence they move towards each other.

NEET Minor Test - 4 - Question 9
Save

A satellite of mass m is orbiting the earth (of radius R) at a height h from its surface. The total energy of the satellite in terms of g0, the value of acceleration due to gravity at the earth’s surface, is
Detailed Solution for NEET Minor Test - 4 - Question 9
Total energy of satellite at height h from the earth surface,

Also,

From eqns. (i) and (ii),

NEET Minor Test - 4 - Question 10
Save

The ratio of escape velocity at earth (ve) to the escape velocity at a planet (vp) whose radius and mean density are twice as that of earth is
Detailed Solution for NEET Minor Test - 4 - Question 10
As escape velocity.

NEET Minor Test - 4 - Question 11
Save

A satellite S is moving in an elliptical orbit around the earth. The mass of the satellite is very small compared to the mass of the earth. Then,
Detailed Solution for NEET Minor Test - 4 - Question 11
The gravitational force on the satellite S acts towards the centre of the earth, so the acceleration of the satellite S is always directed towards the centre of the earth.
NEET Minor Test - 4 - Question 12
Save

A black hole is an object whose gravitational field is so strong that even light cannot escape from it. To what approximate radius would earth (mass = 5.98 × 1024kg) have to be compressed to be a black hole?
Detailed Solution for NEET Minor Test - 4 - Question 12
Light cannot escape from a black hole,vesc = c

= 8.86 × 10−3m ≈ 10−2m

NEET Minor Test - 4 - Question 13
Save

Infinite number of bodies, each of mass 2 kg are situated on x-axis at distances 1 m, 2 m, 4 m, 8 m ,..., respectively, from the origin. The resulting gravitational potential due to this system at the origin will be
Detailed Solution for NEET Minor Test - 4 - Question 13
The resulting gravitational potential at the origin O due to each of mass 2 kg located at positions as shown in figure is

=

= -4G

NEET Minor Test - 4 - Question 14
Save

The radius of a planet is twice the radius of earth. Both have almost equal average mass-densities. VP and VE are escape velocities of the planet and the earth, respectively, then
Detailed Solution for NEET Minor Test - 4 - Question 14

Here, Rp = 2RE, ρE=ρP

Escape velocity of the earth, VE

=

Escape velocity of the planet

Divide (i) by (ii), we get

NEET Minor Test - 4 - Question 15
Save

The height at which the weight of a body becomes 1/16th its weight on the surface of earth (radius R), is
Detailed Solution for NEET Minor Test - 4 - Question 15
Acceleration due to gravity at a height h from the surface of earth is

where g is the acceleration due to gravity at the surface of earth and R is the radius of earth.

Multiplying by m (mass of the body) on both sides in (i), we get

∴ Weight of body at height h ,W′ = mg′

Weight of body at surface of earth, W = mg

According to question,W′ = 1/16W

or h/R = 3 or h = 3R

NEET Minor Test - 4 - Question 16
Save

The total mechanical energy of a spring-mass system in simple harmonic motion is E = 1/2mω2A2. Suppose the oscillating particle is replaced by another particle of double the mass while the amplitude A remains the same. The new mechanical energy will
Detailed Solution for NEET Minor Test - 4 - Question 16

Total energy depends on k of spring and amplitude A. It is independent of mass.

NEET Minor Test - 4 - Question 17
Save

A body describes simple harmonic motion with an amplitude of 5 cm, and a period of 0.2 s. Find the acceleration and velocity of the body when the displacement is 3 cm, and when the displacement is zero.
Detailed Solution for NEET Minor Test - 4 - Question 17
Given, amplitude,

A = 5 cm = 0.05 m

Time period,

T= 0.2 s

When the displacement is x = 3 cm = 0.03 m, the acceleration is,

A = −ω2x

Velocity is,

When the displacement is x = 0, acceleration a = −ω2x = 0.

Velocity,

NEET Minor Test - 4 - Question 18
Save

A particle of mass m oscillates with simple harmonic motion between points x1 and x2, the equilibrium position being O. Its potential energy is plotted. It will be as given below in the graph
Detailed Solution for NEET Minor Test - 4 - Question 18
Potential energy of particle performing SHM varies parabolically in such a way that at mean position it becomes zero and maximum at extreme position.
NEET Minor Test - 4 - Question 19
Save

Two simple harmonic motions of angular frequency 100 and 1000 rad s–1 have the same displacement amplitude. The ratio of their maximum acceleration is
Detailed Solution for NEET Minor Test - 4 - Question 19

NEET Minor Test - 4 - Question 20
Save

The displacement of a particle along the x-axis is given by x = asin2ωt. The motion of the particle corresponds to
Detailed Solution for NEET Minor Test - 4 - Question 20

x = asin2ωt

On comparing (1)1 with the standard sinusoidal equation of SHM, we get,

We conclude that the given equation represents the simple harmonic motion of amplitude a/2 and angular frequency 2ω.

NEET Minor Test - 4 - Question 21
Save

The circular motion of a particle with constant speed is
Detailed Solution for NEET Minor Test - 4 - Question 21
In a circular motion particle repeats after equal intervals of time. So particle motion on a circular path is periodic but not simple harmonic as it does not execute to and fro motion about a fixed point.
NEET Minor Test - 4 - Question 22
Save

A body is vibrating in simple harmonic motion. If its acceleration is 12 cm s−2 at a displacement 3 cm, then time period is
Detailed Solution for NEET Minor Test - 4 - Question 22

Here a = 12 cm s−2 at x = 3 cm

In SHM, acceleration a = −ω2x

∴ Magnitude of acceleration a = ω2x

(discarding off -ve sign)

NEET Minor Test - 4 - Question 23
Save

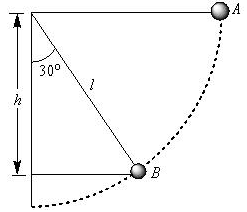
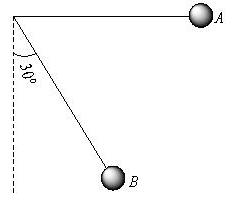
A simple pendulum is released from A shown.

If m and l represent the mass of the bob and Length of the pendulum, the gain kinetic energy at B is
Detailed Solution for NEET Minor Test - 4 - Question 23
Loss of potential energy in coming from A to B

= mgh

= mglcos30° = √3 / 2 mgl

Kinetic energy gained = loss of potential energy

= √3 / 2 mgl

NEET Minor Test - 4 - Question 24
Save

For Simple Harmonic Oscillator, the potential energy is equal to kinetic energy
Detailed Solution for NEET Minor Test - 4 - Question 24
potential energy U and kinetic energy K in SHM are given by

where

m = mass of particle

ω = angular frequency of particle executing SHM

A = amplitude of SHM

X = displacement of particle from mean position

equating both

K = U

hence When a particle executes SHM, there will be two position in each cycle where the PE is equal to KE of the body in SHM

NEET Minor Test - 4 - Question 25
Save

A particle is vibrating in simple harmonic motion with an amplitude of 4 cm. At what displacement from the equilibrium position is its energy half potential and half kinetic?
Detailed Solution for NEET Minor Test - 4 - Question 25
The total energy E of a particle vibrating SHM is given by

The kinetic energy K is given by

where y = displacements of the particle

But,

Hence the kinetic energy is half of the total energy when displacement of the particle is a/√2. Given that a = 4cm.

NEET Minor Test - 4 - Question 26
Save

If the initial tension on a stretched string is doubled, then the ratio of the initial and final speeds of a transverse wave along the string is
Detailed Solution for NEET Minor Test - 4 - Question 26
We know, velocity of transverse wave

NEET Minor Test - 4 - Question 27
Save

In a guitar, two strings A and B made of same material are slightly out of tune and produce beats of frequency 6Hz. When tension in B is slightly decreased, the beat frequency increases to 7Hz. If the frequency of A is 530Hz, the original frequency of B will be
Detailed Solution for NEET Minor Test - 4 - Question 27
Frequency of string,

Frequency ∝ √ Tension

Difference of fA and fB is 6 Hz.

If tension decreases, fB decreases and becomes fB′

Now, difference of fA and fB′ = 7Hz (increases) So,fA > fB

fA − fB = 6Hz

⇒ fA = 530Hz

⇒fB = 524Hz (original)

NEET Minor Test - 4 - Question 28
Save

A tuning fork is used to produce resonance in a glass tube. The length of the air column in this tube can be adjusted by a variable piston. At room temperature of 27∘C two successive resonances are produced at 20cm and 73cm of column length. If the frequency of the tuning fork is 320Hz, the velocity of sound in air at 27∘C is
Detailed Solution for NEET Minor Test - 4 - Question 28
The velocity of sound in air at 27°C is v = 2(v)[L2 − L1]; where v = frequency of tuning fork and L1, L2 are the successive column length.

∴ v = 2 × 320[73 − 20] × 10−2

= 339.2ms−1 ≈ 339ms−1.

NEET Minor Test - 4 - Question 29
Save

The two nearest harmonics of a tube closed at one end and open at other end are 220 Hz and 260 Hz. What is the fundamental frequency of the system?
Detailed Solution for NEET Minor Test - 4 - Question 29
Nearest harmonics of an organ pipe closed at one end is differ by twice of its fundamental frequency.

∴ 260 − 220 = 2υ, υ = 20 Hz

NEET Minor Test - 4 - Question 30
Save

The second overtone of an open organ pipe has the same frequency as the first overtone of a closed pipe L metre long. The length of the open pipe will be
Detailed Solution for NEET Minor Test - 4 - Question 30

Second overtone of an open organ pipe

=Third harmonic = 3 × υ′0 = 3 × v/2L′

First overtone of a closed organ pipe

= Third harmonic = 3 × υ0 = 3 × v/4L

According to question,

3υ′0 = 3υ0 ⇒3 × v/2L′ = 3 × v/4L

⇒ L′ = 2L

View more questions
1 videos|26 docs|121 tests
Join Course
Information about NEET Minor Test - 4 Page
In this test you can find the Exam questions for NEET Minor Test - 4 solved & explained in the simplest way possible. Besides giving Questions and answers for NEET Minor Test - 4, EduRev gives you an ample number of Online tests for practice

Top Courses for NEET

1 videos|26 docs|121 tests
Join Course
Download as PDF

Top Courses for NEET

Important Questions for NEET Minor Test - 4

Find all the important questions for NEET Minor Test - 4 at EduRev.Get fully prepared for NEET Minor Test - 4 with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the NEET Minor Test - 4 syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of NEET Minor Test - 4 resources.

NEET Minor Test - 4 MCQs with Answers

Prepare for the NEET Minor Test - 4 within the NEET exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for NEET Minor Test - 4 NEET Mock Test Series 2025

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace NEET Minor Test - 4 with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Follow Us
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup