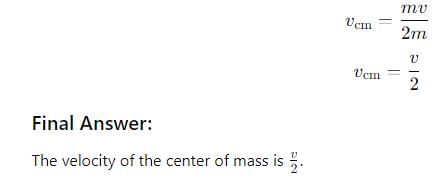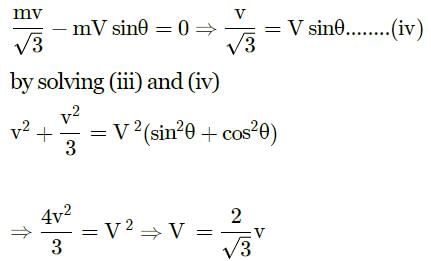Explore Exams
Login Signup
Sign in Open App
NEET Exam  >  NEET Test  >  Physics Class 11  >  NEET Previous Year Questions: Centre of Mass - NEET MCQ

NEET Previous Year Questions: Centre of Mass Free MCQ Test with solutions


MCQ Practice Test & Solutions: NEET Previous Year Questions: Centre of Mass (12 Questions)

You can prepare effectively for NEET Physics Class 11 with this dedicated MCQ Practice Test (available with solutions) on the important topic of "NEET Previous Year Questions: Centre of Mass". These 12 questions have been designed by the experts with the latest curriculum of NEET 2026, to help you master the concept.

Test Highlights:

  • - Format: Multiple Choice Questions (MCQ)
  • - Duration: 12 minutes
  • - Number of Questions: 12

Sign up on EduRev for free to attempt this test and track your preparation progress.

NEET Previous Year Questions: Centre of Mass - Question 1
Save

Two identical particles move towards each other with velocity 2v and vrespectively. The velocity of centre of mass is  [AIEEE 2002]

Detailed Solution: Question 1

NEET Previous Year Questions: Centre of Mass - Question 2
Save

 Consider the following two statements :

A. Linear momentum of a system of particles is zero.

B. kinetic energy of a system of particles is zero.Then 

[AIEEE 2003]

Detailed Solution: Question 2

- Statement A states that the linear momentum of a system is zero. This means that the total momentum is balanced, but individual particles can still be moving.
- Statement B states that the kinetic energy of the system is zero. This would only occur if all particles are at rest.
- If A is true (momentum is zero), B isn't necessarily true (kinetic energy can be non-zero).
- If B is true (kinetic energy is zero), A must be true (momentum must also be zero).
- Therefore, the correct choice is that A does not imply B, but B implies A.

Clear all your doubts with EduRev
NEET Previous Year Questions: Centre of Mass - Question 3
Save

A body A of mass M while falling vertically downwards under gravity breaks into two parts; a body B of mass 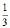 M and, a body C of mass M. The centre of mass of bodies B and C taken together shifts compared to that of body A towards 

 [AIEEE 2005]

Detailed Solution: Question 3

Since there is no different external force applied to the individual particles, the centre of mass remains same and does not shift.

NEET Previous Year Questions: Centre of Mass - Question 4
Save

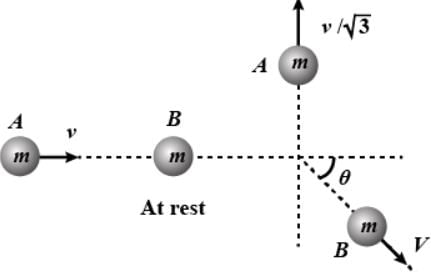
A mass m moves with a velocity v and collides inelastically with another identical mass. After collision the 1st mass moves with velocity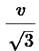 in a direction perpendicular to the initial direction of motion. Find the speed of the second mass after collision.   

[AIEEE 2005]

Detailed Solution: Question 4

Let mass A moves with velocity v and collides inelastically with mass B, which is at rest.  
According to problem mass A moves in a perpendicular direction and let the mass B moves at angle θ with the horizontal with velocity v.
Initial horizontal momentum of system 
(before collision) = mv ....(i) 
Final horizontal momentum of system 
(after collision ) = mVcosθ.................(ii)
From the conservation of horizontal linear momentum mv
= mvcosθ ⇒ v = Vcosθ .....(iii) 
Initial vertical momentum of system (before collision) is zero.
Final vertical momentum of system mv/√3 − mV sinθ
From the conservation of vertical linear momentum 

NEET Previous Year Questions: Centre of Mass - Question 5
Save

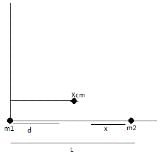
 Consider a two particle system with particles having masses m1 and m2. If the first particle is pushed towards the centre of mass through a distance d, by what distance should the second particle be moved, so as to keep the centre of mass at the same position?  

[AIEEE 2006]

Detailed Solution: Question 5


Xcm = (m1x1 + m2x2)/(m1 + m2)
Xcm = m2L/(m1 + m2)
Now, ATQ
Xcm = (m1d + m2(L-x))/(m1 + m2)
Since Xcm is same so,
⇒ (m1d + m2(L-x))/(m1 + m2) = m2L/(m1 + m2)
⇒ m1d + m2L - m2x = m2L
⇒ m1d = m2x
⇒ x = m1d/m2

NEET Previous Year Questions: Centre of Mass - Question 6
Save

A bomb of mass 16 kg at rest explodes into two pieces of masses 4 kg and 12 kg. The velocity of the 12 kg mass is 4 ms-1. The kinetic energy of the other mass is

[AIEEE 2006]

Detailed Solution: Question 6

Applying Conservation of Linear Momentum
16 x 0 = 12 x 4 + 4 x v => v = -12 m/s
So, KE = ½ m v2 = ½ x 4 x 144 = 288J

NEET Previous Year Questions: Centre of Mass - Question 7
Save

A player caught a cricket ball of mass 150 g moving at a rate of 20 m/s. If the catching process is completed in 0.1 s, the force of the blow exerted by the ball on the hand of the player is equal to

 [AIEEE 2006]

Detailed Solution: Question 7

F = ma = m(v/t)
F = 150 × 20 / 0.1 × 1000
F = 30N

NEET Previous Year Questions: Centre of Mass - Question 8
Save

A circular disc of radius R is removed from a bigger circular disc of radius 2 R, such that the circumference of the discs coincide. The centre of mass of the new disc is  from the centre of the bigger disc. The value of a is

[AIEEE 2007]

Detailed Solution: Question 8

NEET Previous Year Questions: Centre of Mass - Question 9
Save

A thin rod of length L is lying along the x-axis with its ends at x = 0 and x = L. Its linear density (mass/length) varies with x as  where n can be zero or any positive number. If the position  of the centre of mass of the rod is plotted against n, which of the following graphs best approximates the dependence of  on n? 

[AIEEE 2008]

NEET Previous Year Questions: Centre of Mass - Question 10
Save

A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is 

 [AIEEE 2008]

Detailed Solution: Question 10

Initial kinetic energy (K.E.) of the system:
Only the 0.50 kg block is moving, so:
K.E.initial = (1/2) x 0.50 x (2.00)2 = 0.25 x 4 = 1.00 J
After collision, both masses move together with a common velocity (v).
Applying conservation of momentum:
Initial momentum = Final momentum
(0.50 x 2.00) + (1.00 x 0) = (0.50 + 1.00) x v
1.00 = 1.50 x v
v = 1.00 / 1.50 = 0.67 m s-1
Final kinetic energy (K.E.):
K.E.final = (1/2) x 1.50 x (0.67)2 ≈ 0.75 x 0.4489 ≈ 0.34 J
Energy lost during collision:
Energy loss = K.E.initial - K.E.final
= 1.00 J - 0.34 J = 0.66 J ≈ 0.67 J
Therefore, the energy loss during the collision is 0.67 J.

NEET Previous Year Questions: Centre of Mass - Question 11
Save

Statement I : Two particles moving in the same direction do not lose all their energy in a completely inelastic collision.

Statement II : Principle of conservation of momentum holds true for all kinds of collisions.

                                                                                                                                 [AIEEE 2010]

Detailed Solution: Question 11

The strong interaction force between two bodies in which momentum is conserved is called collision. In any type of collision momentum is always conserved kinetic energy may or may not be conserved.

NEET Previous Year Questions: Centre of Mass - Question 12
Save

 Statement-I : A point particle of mass m moving with speed u collides with stationary point particle of mass M. If the maximum energy loss possible is given as  then f = .

Statement-II : Maximum energy loss occurs when the particles get stuck together as a result of the collision.                                      [JEE MAIN 2013]

97 videos|376 docs|98 tests
Join Course
Information about NEET Previous Year Questions: Centre of Mass Page
In this test you can find the Exam questions for NEET Previous Year Questions: Centre of Mass solved & explained in the simplest way possible. Besides giving Questions and answers for NEET Previous Year Questions: Centre of Mass, EduRev gives you an ample number of Online tests for practice
97 videos|376 docs|98 tests
Join Course
Download as PDF
;

About this NEET Practice Test

This test contains 12 MCQs on NEET Previous Year Questions: Centre of Mass with detailed solutions for each question. It is part of the Physics Class 11 course on EduRev, designed to align with the current NEET syllabus. Each solution explains not just the correct answer but also gives you an understanding of the topic — not just to attempt the question but also help you prepare for the exam with practice.

Explore more NEET Study Resources

If you found this NEET Previous Year Questions: Centre of Mass MCQ Test helpful, you can further enhance your NEET preparation with in-depth courses on EduRev, for all the subjects and topics available in Physics Class 11 course. The course offers:
  • Video Lectures: covering all the topics of Physics Class 11
  • Notes for Revision: offering revision notes, important questions, summaries, flashcards, cheatsheets & more for NEET preparation
  • MCQ Test: variety of questions as per the pattern of NEET exam
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily