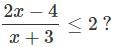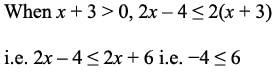NMAT Quantitative Skills MCQ Quiz - 1 - CAT MCQ
30 Questions MCQ Test - NMAT Quantitative Skills MCQ Quiz - 1
Group Question
Answer the following question based on the information given below.
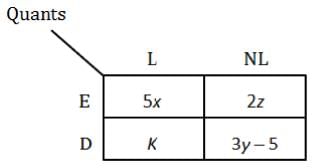
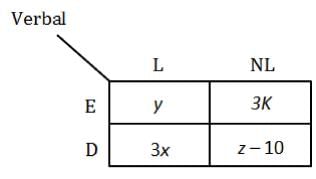
In an MBA entrance exam, questions are classified into two sections - Quants and Verbal. The number of questions in Quants is less than 100 while that in Verbal is not less than 75. Within each section, the questions are classified into Easy or Difficult based on the number of concepts involved. An easy question requires not more than 1 concept, while a difficult question requires 2 or more concepts to solve.Further, a question could be lengthy (atleast 3 minutes to solve) or non- lengthy (less thanl minute to solve).
Based on the following data, answer the subsequent questions.
1. The number of difficult, non-lengthy questions in Verbal is 10 less than half the number of easy, non-lengthy questions in Quants.
2. The ratio of number of easy, lengthy questions in Quants to number of difficult, lengthy questions in Verbal is 5:3.
3. The number of non-lengthy, difficult questions in Quants is 5 less than thrice the number of lengthy, easy questions in Verbal.
4. The number of lengthy questions in Verbal is 35 less than the number of easy questions in Quant.
5. The number of non-lengthy questions in Quants is 30 more than the number of difficult questions in Verbal.
6. The number of easy, non lengthy question in Verbal is thrice the number of lengthy, difficult questions in Quant.
7. Each sub-section had atleast 5 questions.
Q.What is the number of easy, but lengthy questions in the Verbal section?
In an MBA entrance exam, questions are classified into two sections - Quants and Verbal. The number of questions in Quants is less than 100 while that in Verbal is not less than 75. Within each section, the questions are classified into Easy or Difficult based on the number of concepts involved. An easy question requires not more than 1 concept, while a difficult question requires 2 or more concepts to solve.Further, a question could be lengthy (atleast 3 minutes to solve) or non- lengthy (less thanl minute to solve).
Based on the following data, answer the subsequent questions.
1. The number of difficult, non-lengthy questions in Verbal is 10 less than half the number of easy, non-lengthy questions in Quants.
2. The ratio of number of easy, lengthy questions in Quants to number of difficult, lengthy questions in Verbal is 5:3.
3. The number of non-lengthy, difficult questions in Quants is 5 less than thrice the number of lengthy, easy questions in Verbal.
4. The number of lengthy questions in Verbal is 35 less than the number of easy questions in Quant.
5. The number of non-lengthy questions in Quants is 30 more than the number of difficult questions in Verbal.
6. The number of easy, non lengthy question in Verbal is thrice the number of lengthy, difficult questions in Quant.
7. Each sub-section had atleast 5 questions.
Q.Which sub-section has the minimum number of questions?
In an MBA entrance exam, questions are classified into two sections - Quants and Verbal. The number of questions in Quants is less than 100 while that in Verbal is not less than 75. Within each section, the questions are classified into Easy or Difficult based on the number of concepts involved. An easy question requires not more than 1 concept, while a difficult question requires 2 or more concepts to solve.Further, a question could be lengthy (atleast 3 minutes to solve) or non- lengthy (less thanl minute to solve).
Based on the following data, answer the subsequent questions.
1. The number of difficult, non-lengthy questions in Verbal is 10 less than half the number of easy, non-lengthy questions in Quants.
2. The ratio of number of easy, lengthy questions in Quants to number of difficult, lengthy questions in Verbal is 5:3.
3. The number of non-lengthy, difficult questions in Quants is 5 less than thrice the number of lengthy, easy questions in Verbal.
4. The number of lengthy questions in Verbal is 35 less than the number of easy questions in Quant.
5. The number of non-lengthy questions in Quants is 30 more than the number of difficult questions in Verbal.
6. The number of easy, non lengthy question in Verbal is thrice the number of lengthy, difficult questions in Quant.
7. Each sub-section had atleast 5 questions.
Q.Which among the following could be a possible value of total number of easy questions?
In an MBA entrance exam, questions are classified into two sections - Quants and Verbal. The number of questions in Quants is less than 100 while that in Verbal is not less than 75. Within each section, the questions are classified into Easy or Difficult based on the number of concepts involved. An easy question requires not more than 1 concept, while a difficult question requires 2 or more concepts to solve.Further, a question could be lengthy (atleast 3 minutes to solve) or non- lengthy (less thanl minute to solve).
Based on the following data, answer the subsequent questions.
1. The number of difficult, non-lengthy questions in Verbal is 10 less than half the number of easy, non-lengthy questions in Quants.
2. The ratio of number of easy, lengthy questions in Quants to number of difficult, lengthy questions in Verbal is 5:3.
3. The number of non-lengthy, difficult questions in Quants is 5 less than thrice the number of lengthy, easy questions in Verbal.
4. The number of lengthy questions in Verbal is 35 less than the number of easy questions in Quant.
5. The number of non-lengthy questions in Quants is 30 more than the number of difficult questions in Verbal.
6. The number of easy, non lengthy question in Verbal is thrice the number of lengthy, difficult questions in Quant.
7. Each sub-section had atleast 5 questions.
Q.Find the maximum possible score of the topper, if each correct option fetches 4 marks?
What is the largest of three consecutive natural numbers if the cube of the first number is smaller than their product by 5, the cube of the second number is greater than their product by 2 and the square of the third number exceeds their product by 3.
From a block of ice cream in the shape of a cuboid of length, breadth and height as a, b, c units respectively, two scoops of ice cream are taken out and served per person. The scoop is in the shape of a hemisphere of radius R. If there is no wastage, how many people get the ice cream?
If Rohan was born on 29th March 1990 on Thursday, on what day on the week will his 25th birthday fall?
An Ant is at (2, 4) and wants to go to (9, 14) but in the process it has to carry food lying on the x-axis. Where should it touch the x-axis, so that it has to cover minimum distance in the entire journey?
Group Question
Answer the following question based on the information given below.
The first pie chart below shows the percentage distribution of three components the weight of a human being while the second pie chart shows the percentage distribution of protein (in terms of weight) across different body parts.



Q.If Zebesco, a professional wrestler, weighs 21 stone, how much of his body weight (in pounds) does not come from protein in tissue?
The first pie chart below shows the percentage distribution of three components the weight of a human being while the second pie chart shows the percentage distribution of protein (in terms of weight) across different body parts.



Q.‘Other nutrients’ in the body comprises minerals, carbohydrates, fats and vitamins in the ratio 2 : 4 : 1 : 3. What is the maximum possible difference (in stone) between the weight contributed by protein in skin and fats for a gymnast weighing 52 kg?
The first pie chart below shows the percentage distribution of three components the weight of a human being while the second pie chart shows the percentage distribution of protein (in terms of weight) across different body parts.

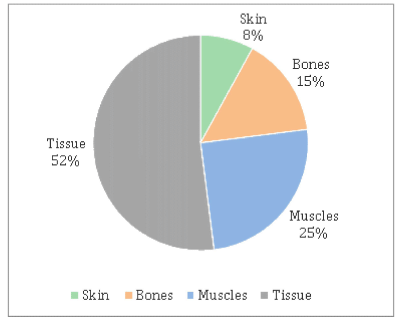

Q.Gaurav weighs 65 kg. What percentage of his body weight comes from muscles?
The first pie chart below shows the percentage distribution of three components the weight of a human being while the second pie chart shows the percentage distribution of protein (in terms of weight) across different body parts.



Q.Which of these is the heaviest component?
Group Question
Answer the following question based on the information given below.
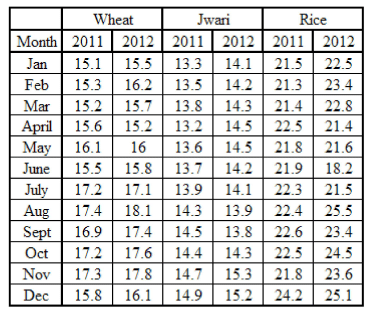
Cereal consumption of Maharashtra state in 000 ton
Q.What is the approximate ratio of the difference between the maximum and minimum monthly wheat consumption for 2011 and the difference between the maximum and minimum monthly rice consumption for 2012?
Answer the following question based on the information given below.
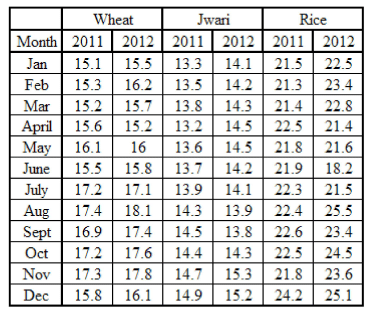
Cereal consumption of Maharashtra state in 000 ton
Q.Which month has highest cereal consumption in 2012?
Answer the following question based on the information given below.
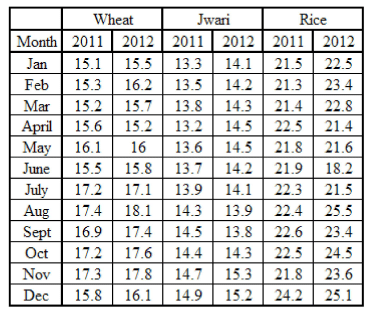
Cereal consumption of Maharashtra state in 000 ton
Q.Which of the following cases shows the maximum instances of a negative percentage change in the monthly consumption?
Answer the following question based on the information given below.
Cereal consumption of Maharashtra state in 000 ton
Q.What is the maximum percentage change in the rice consumption for the year 2011?
There is a field which is in the shape of a quarter circle. A cow is tied on the field such that the circle formed by its grazing is exactly inscribed in the quarter. What is the ratio of area which is grazed and that which is not?
A toy is made by mounting a hemisphere of radius 7 cm over a right circular cylinder of the same radius. (Flat surface of hemisphere coincides with that of the right circular cylinder.) Height of the clinder is 10 cm. What will be the cost of painting the entire toy except the base, if the cost of painting is Rs. 14 per cm2?
Arun and Ram work together and complete the construction of a wall in x days. When Arun works alone, he takes 18 more days than x. When Ram works alone, he takes 8 more days than x. If they are paid an amount of Rs. 600 for the entire work in proportion to their work done, what is the difference between the amounts that Aran and Ram receive?
In a triangle ABC, AD is the median to BC. If AB = BC = 12 cm and AC = 8 cm, AD = ?
2500 students gave an examination comprising five questions. Each question had five answer choices, of which only one was correct. The marking scheme was +4/-1 for every correct/incorrect answer. Each student attempted all the questions. If the overall answer key of no two students was the same, what is the minimum number of students with a positive score?
The total number of chocolates with Ram and Lakhan is more than 85 but less than 95. If Lakhan gives a particular number of chocolates to Ram, then Ram will have eight times the number of chocolates left with Lakhan and if Ram gives the same number of chocolates to Lakhan, then Lakhan will have double the number of chocolates left with Ram. How many chocolates does Ram have?
How many six-digit numbers are there such that the 3rd digit is the square of the 1st digit and the 4th digit is the square of the 2nd digit?
Group Question
Answer the following question based on the information given below.
The chart below shows the selling price (in Rs. 000s) of plywood, saw timber and logs. The price of logs is per cubic metre and while that of plywood and saw timber is per tonne. All prices are integral.
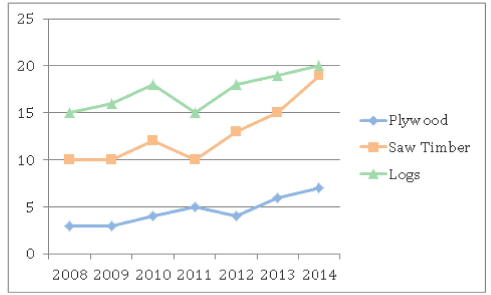
1 cubic metre of plywood = 1 cubic metre of saw timber = 800 kg
Q.How many cubic metres of plywood would have to be sold in 2011 to yield the same revenue as generated from the sales of 220 tonnes of saw timber in 2014?
The chart below shows the selling price (in Rs. 000s) of plywood, saw timber and logs. The price of logs is per cubic metre and while that of plywood and saw timber is per tonne. All prices are integral.
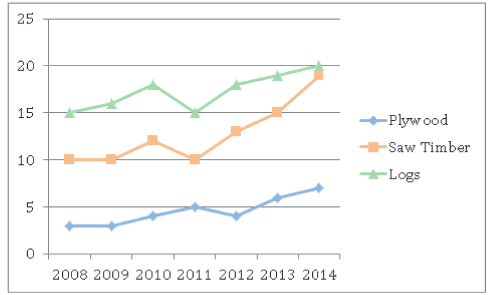
1 cubic metre of plywood = 1 cubic metre of saw timber = 800 kg
Q.In which year is the total selling price of 1 cubic metre of each of the three products the least?
The chart below shows the selling price (in Rs. 000s) of plywood, saw timber and logs. The price of logs is per cubic metre and while that of plywood and saw timber is per tonne. All prices are integral.

1 cubic metre of plywood = 1 cubic metre of saw timber = 800 kg
Q.In 2010, what is the ratio of the selling price per tonne for plywood, logs and saw timber?
The chart below shows the selling price (in Rs. 000s) of plywood, saw timber and logs. The price of logs is per cubic metre and while that of plywood and saw timber is per tonne. All prices are integral.
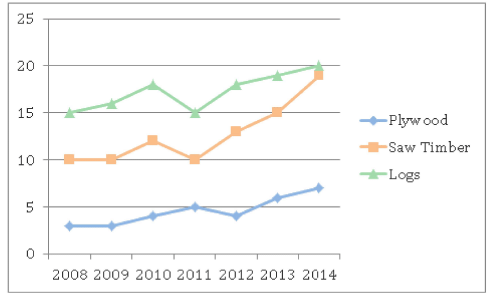
1 cubic metre of plywood = 1 cubic metre of saw timber = 800 kg
Q.In 2012, if plywood, saw timber and logs contributed to 20%, 30% and 50% of the total sales (by cubic metre), what was the average selling price (in Rs. 000s) per cubic metre?
Group Question
Answer the following question based on the information given below.
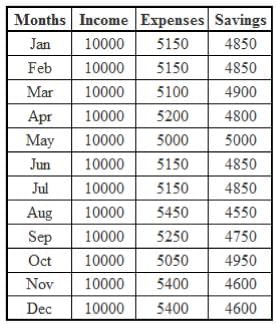
The expenses of a particular household fall under 4 broad headings, as shown below.
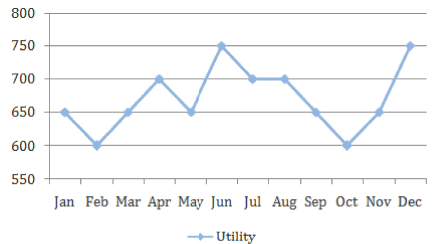
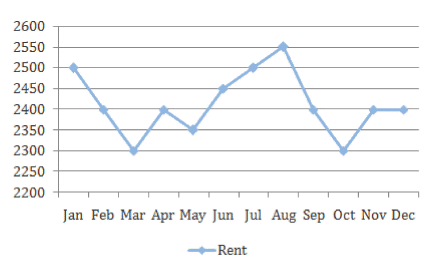
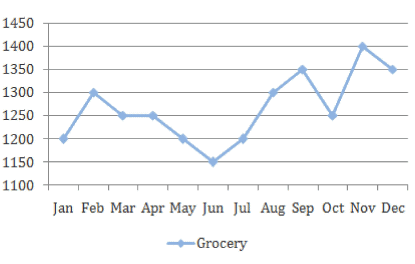
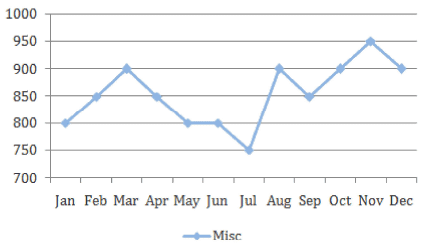
The overall monthly expenditure of the household is the sum of the individual expenditure on each head in the month. All figures in the graphs are in actuals.
The income of this household is constant at Rs. 10,000 per month. Any unspent amount is saved in this household.
Q.In which month are the savings highest for the household?