NMAT Quantitative Skills MCQ Quiz - 3 - CAT MCQ
30 Questions MCQ Test - NMAT Quantitative Skills MCQ Quiz - 3
S is the set of all possible permutations of the letters of the word APPLE. In how many of these permutations does the letter A come before the letter P?
Answer the following question based on the information given below.
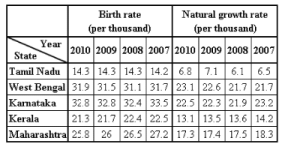
The first table shows the birth rate and natural growth rate per thousand in a country.
The second table shows the infant mortality rate.
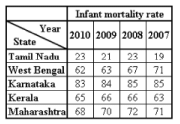
Natural growth rate = Birth rate - Death rate and Infant Mortality rate = number of infant deaths per thousand births
Q.
If the population of Maharashtra on 1st January, 2009 was 100 crores, what was the population of Maharashtra on 31st December 2010 (in crores)?
The first table shows the birth rate and natural growth rate per thousand in a country.
If an infant death is defined as the death of a child on the very day that it is bom, then approximately what percent of the total deaths in Maharashtra are infant deaths in the year 2009?
Which of the following states recorded the highest percentage decrease in death rate over the entire period?
Which state never saw a decrease in birth rates over the given period?
Group Question Answer the following question based on the information given below.
The chart below shows the income and expenditure (in Rs. crores) of a firm for four successive quarters in an year.
Q.
The profit earned by the firm in Q1 is invested at the start of Q2 in T-bills at simple interest at 8% per annum for three months. What is the total profit made by the firm (in Rs. crores) at the end of Q2?
Group Question Answer the following question based on the information given below.
The chart below shows the income and expenditure (in Rs. crores) of a firm for four successive quarters in an year.
Q.
For Q1 of the next year, the income is the average quarterly income of the previous year and the expenditure is the average quarterly expenditure of the previous year. What is the profit generated (in Rs. crores) in Q1 of the next year?
Group Question Answer the following question based on the information given below.
The chart below shows the income and expenditure (in Rs. crores) of a firm for four successive quarters in an year.
Q.
What is the maximum percentage profit earned by the company in any of the given quarters?
Group Question Answer the following question based on the information given below.
The chart below shows the income and expenditure (in Rs. crores) of a firm for four successive quarters in an year.
Q.
What is the income (in Rs. crores) in Ql of the next year, if the expenditure in that quarter is the same as the expenditure in Q4 this year, while the percentage profit has gone up by 5 percentage points from Q4 this year?
Group Question Answer the following question based on the information given below.
The chart below shows the income and expenditure (in Rs. crores) of a firm for four successive quarters in an year.
Q.
A circle of maximum area is cut out from a square cardboard of side a cm. The cardboard left is thrown away. Now, a right angled triangle is cut out from the circle such that all three vertices of the triangle lie on the circumference of the circle and touch the sides of the square. Again the cardboard left is thrown away. What is the ratio of the area of the triangular cardboard to the area of the cardboard that is thrown away?
Group Question Answer the following question based on the information given below.
The chart below shows the income and expenditure (in Rs. crores) of a firm for four successive quarters in an year.
Q.
The weight of a circular disc is proportional to the square of the radius of the disc when the thickness of the disc is kept constant, whereas the weight of the disc is proportional to its thickness when the radius of the disc is kept constant.
What is the ratio of the radii of two circular discs, if their thicknesses are in the ratio 9 : 8 and their weights are in the ratio 2 : 1 ?
Nine members of a family are standing in a row. Their average age is 70. The average age of the first four members in the row is 64 and the average age of the last seven members in the row is 80. What is the average age of the third and fourth member in the row?
Group Question
Answer the following question based on the information given below.
The charts below show the performance of cricket teams from various cities. The matches won, drawn and lost are given in percentage terms in the bar graph. The total number of matches played by various teams is not necessarily the same.
Q.
What is the total number of matches played by Indore, Chennai, Ludhiana, Bangalore and Kolkata?
Group Question
Answer the following question based on the information given below.
The charts below show the performance of cricket teams from various cities. The matches won, drawn and lost are given in percentage terms in the bar graph. The total number of matches played by various teams is not necessarily the same.
Q.
By what percent is the number of matches drawn by Banglore more/less than the number of matches lost by Chandigarh?
Group Question
Answer the following question based on the information given below.
The charts below show the performance of cricket teams from various cities. The matches won, drawn and lost are given in percentage terms in the bar graph. The total number of matches played by various teams is not necessarily the same.
Q.
What is the difference between the number of matches lost by Pune and Ludhiana? 1)12
2 ) 14
3 ) 10
4 ) 9
5 ) 13
Group Question
Answer the following question based on the information given below.
The charts below show the performance of cricket teams from various cities. The matches won, drawn and lost are given in percentage terms in the bar graph. The total number of matches played by various teams is not necessarily the same.
Q.
What is the difference between the total number of matches won by all the teams and the total number of matches drawn by all the teams?
Group Question
Answer the following question based on the information given below.
The charts below show the performance of cricket teams from various cities. The matches won, drawn and lost are given in percentage terms in the bar graph. The total number of matches played by various teams is not necessarily the same.
Q.
There is a match box of dimensions 10 cm x 6 cm x 2 cm. What is the maximum length of the match-stick that can be kept inside it?
Group Question
Answer the following question based on the information given below.
The charts below show the performance of cricket teams from various cities. The matches won, drawn and lost are given in percentage terms in the bar graph. The total number of matches played by various teams is not necessarily the same.
Q.
A and B work on a project on alternate days. If A starts the project, they complete 7/10th of the work in 9 days. If B starts the project, they complete 5/6th of the work in 10 days. If B were to work alone, how many days would he take to complete the project?
Group Question
Answer the following question based on the information given below.
The charts below show the performance of cricket teams from various cities. The matches won, drawn and lost are given in percentage terms in the bar graph. The total number of matches played by various teams is not necessarily the same.
Q.
What will be the value of the following expression if x = 21/2 ?
Each question is followed by two statements, A and B. Answer each question using the following instructions:
Mark option (1) if the question can be answered by using statement A alone but not by using statement B alone.
Mark option (2) if the question can be answered by using statement B alone but not by using statement A alone.
Mark option (3) if the question can be answered by using either statement alone.
Mark option (4) if the question can be answered by using both the statements together but not by either of the statements alone.
Mark option (5) if the question cannot be answered on the basis of the two statements.
A boy plucked 15 mangoes in 4 days. On the first day, he plucked 4 mangoes. Find the number of mangoes that he plucked on each day (ignoring the order in which they were plucked), if he plucked at least one mango every day.
A. He plucked an odd number of mangoes on each of the remaining days.
B. He plucked an equal number of mangoes on no two days.
Each question is followed by two statements, A and B. Answer each question using the following instructions:
Mark option (1) if the question can be answered by using statement A alone but not by using statement B alone.
Mark option (2) if the question can be answered by using statement B alone but not by using statement A alone.
Mark option (3) if the question can be answered by using either statement alone.
Mark option (4) if the question can be answered by using both the statements together but not by either of the statements alone.
Mark option (5) if the question cannot be answered on the basis of the two statements. The ages of Jai and Veeru are in the ratio of 2 : 1 .What is the age of Veeru?
A. The ages of Veeru and Gabbar are in the ratio of 2 : 1
B. After 4 years the ratio of Jai and Veeru’s ages will be 3 : 2
Each question is followed by two statements, A and B. Answer each question using the 3 following instructions:
Mark option (1) if the question can be answered by using statement A alone but not by using statement B alone.
Mark option (2) if the question can be answered by using statement B alone but not by
using statement A alone.
Mark option (3) if the question can be answered by using either statement alone.
Mark option (4) if the question can be answered by using both the statements together but not by either of the statements alone.
Mark option (5) if the question cannot be answered on the basis of the two statements. What is the profit percent obtained by selling each pen?
A. By selling x pens at Rs. x per pen, shopkeeper earns a profit of Rs. 150.
B. Pens are brought at Rs. x per gross and are sold at Rs. x/8 per pen. (1 gross = 12 pens)
Each question is followed by two statements, A and B. Answer each question using the following instructions:
Mark option (1) if the question can be answered by using statement A alone but not by using statement B alone.
Mark option (2) if the question can be answered by using statement B alone but not by using statement A alone.
Mark option (3) if the question can be answered by using either statement alone.
Mark option (4) if the question can be answered by using both the statements together but not by either of the statements alone.
Mark option (5) if the question cannot be answered on the basis of the two statements. What is the speed of the cruise ship when sailing in still water?
A. It passes a lighthouse tower (of negligible length) in 10 seconds.
B. It passes another cruise ship of length 600 metres in 30 seconds
The question is followed by two statements, A and B. Answer each question using the following instructions: Mark option (1) if the question can be answered by using the statement A alone but not by using the statement II alone.
Mark option (2) if the question can be answered by using the statement B alone but not by using the statement I alone.
Mark option (3) if the question can be answered by using either of the statements alone. Mark option (4) if the question can be answered by using both the statements together but not by either of the statements alone.
Mark option (5) if the question cannot be answered on the basis of the two statements.
If p and m - 8 are positive integers, is p/m less than one?
A. p - m > 0
B.p < 8
Each question is followed by two statements, A and B. Answer each question using the following instructions: Mark option (1) if the question can be answered by using statement A alone but not by using statement B alone.
Mark option (2) if the question can be answered by using statement B alone but not by using statement A alone.
Mark option (3) if the question can be answered by using either statement alone.
Mark option (4) if the question can be answered by using both the statements together but not by either of the statements alone.
Mark option (5) if the question cannot be answered on the basis of the two statements. What is the value of the positive integer N.
A. Sum of all the factors of N, excluding itself, is 56.
B. The total number of factors A has is 4.
What is the remainder when 1! + 2! + 3! + 4! + ... + 55! is divided by 12?
If m and n are two natural numbers, ratio of m to n is x and ratio of n to m is y, then (x + y) will be
Esha is 28 years old. She is twice as old as Ankita was when Esha was as old as Ankita is now. How old is Ankita now?














