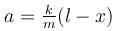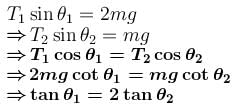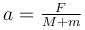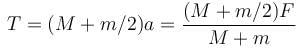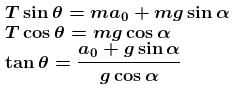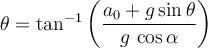Newton's Law Of Motion MCQ Level - 2 - IIT JAM MCQ
10 Questions MCQ Test - Newton's Law Of Motion MCQ Level - 2
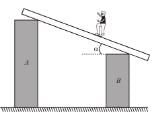
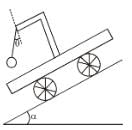
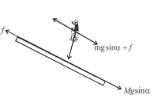
A plank is held at an angle α to the horizontal (Figure) on two fixed supports A and B. The plank can slide against the supports (without friction) because of its weight Mg. Find the acceleration and direction in which a man of mass m should move so that the plank does not move.

A particle of mass 2kg moves with an initial velocity of  on the xy-plane. A force
on the xy-plane. A force acts on the particle. The initial position of the particle is (2m, 3m). Then for y = 3m,
acts on the particle. The initial position of the particle is (2m, 3m). Then for y = 3m,
 on the xy-plane. A force
on the xy-plane. A force acts on the particle. The initial position of the particle is (2m, 3m). Then for y = 3m,
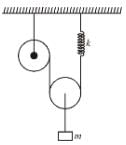
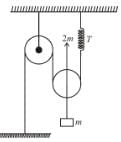
acts on the particle. The initial position of the particle is (2m, 3m). Then for y = 3m,Mass m shown in the figure is in equilibrium. If it is displaced further by x and released, find its acceleration just after it is released. Take pulleys to be light and smooth and string light.

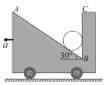
A block of mass m lies on wedge of mass M, which lies on fixed horizontal surface. The wedge is free to move on the horizontal force of magnitude F is applied on block as shown, neglecting friction at all surfaces, the value of force F such that block has no relative motion w.r.t. wedge will be : (where g is acceleration due to gravity)

In the figure shown the acceleration of A is,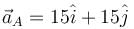 then the acceleration of B is : (A remains in contact with B)
then the acceleration of B is : (A remains in contact with B)
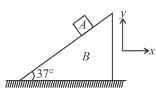
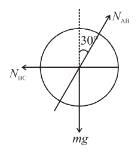
A cylinder rest in a supporting carriage as shown. The side AB of carriage makes an angle 30° with the horizontal and side BC is vertical. The carriage lies on a fixed horizontal surface and is being pulled towards left with an horizontal acceleration a. The magnitude of normal reactions exerted by sides AB and BC of carriage on the cylinder be NAB and NBC respectively. Neglect friction everywhere. Then as the magnitude of acceleration a of the carriage is increased, pick up the correct statement :
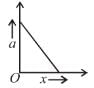
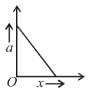
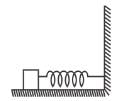
A light spring is compressed and placed horizontally between a vertical fixed wall and a block free to slide over a smooth horizontal table top as shown in the figure. The system is released from rest. The graph which represents the relation between the magnitude of acceleration a of the block and the distance x traveled by it (as long as the spring is compressed) is :
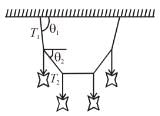
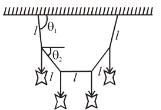
Four identical metal butterflies are hanging from a light string of length 5l at equally placed points as shown in the figure. The ends of the string are attached to a horizontal fixed support. The middle section of the string is horizontal. The relation between the angle θ1 and θ2 is given by :
A block is lying on the horizontal frictionless surface. One end of a uniform rope is fixed to the block which is pulled in the horizontal direction by applying a force F at the other end. If the mass of the rope is half the mass of the block, the tension in the middle of the rope will be
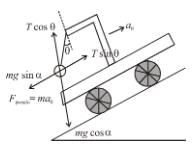
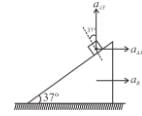
A pendulum of mass m hangs from a support fixed to a trolley. The direction of the string when the trolley rolls up a plane of inclination  with acceleration a0 is :
with acceleration a0 is :


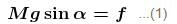
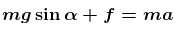 ........(2)
........(2)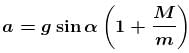 down the incline
down the incline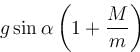 down the incline
down the incline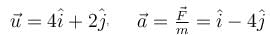
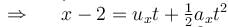 and
and 
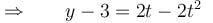

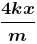

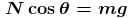 ...(1)
...(1)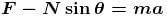 ......(2)
......(2)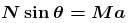 ...(3)
...(3)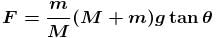
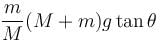

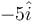
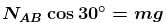
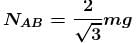 ......(1)
......(1)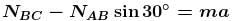
 ...(2)
...(2)