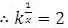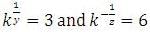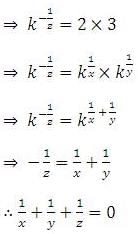Number System - Olympiad Level MCQ, Class 9 Mathematics - Class 9 MCQ
25 Questions MCQ Test - Number System - Olympiad Level MCQ, Class 9 Mathematics
Find the remainder when 73 x 75 x 78 x 57 x 197 x 37 is divided by 34.
Arrange in descending order √8, ∛81 , ∛250
Value of (256)0.16 x (256)0.09=?
Which one of the following is a rational number ?
Which of the following is not an improper fraction :-
Let N = 1421*1423*1425. What is the remainder when N is divided by 12?
Find the least number which will leaves remainder 5 when divided by 8, 12, 16 and 20.
The binary equivalent of (1011.011)10 is equal to
If pqr = 1, then is equal to :-
What is the sum of all two digit numbers that gives a remainder of 3 when they are divided by 7?
The exponential form of is :-
If A =  , then the value of
, then the value of is :-
If x = and y = 1, the value of
is :-
If a = , b =
then value of a3 + b3 is :-
If 2x = 3y = 6-z, then is equal to :-
If ax = b, by = c and cz = a, then the value of xyz is :-
Solution set of the equation |x – 2| = 5 is :-
Three numbers are in ratio 1:2:3 and HCF is 12. The numbers are:
The minimum value of the expression |17x – 8 | – 9 is :-
If 2a – 9 = b + a, then the value of (|a – b| + |b – a|) is :-
If the decimal number is a fraction then its binary equivalent is obtained by ________ the number continuously by 2.