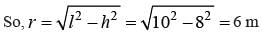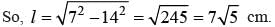Olympiad Test: Elementary Mensuration-II - 1 - Class 7 MCQ
20 Questions MCQ Test - Olympiad Test: Elementary Mensuration-II - 1
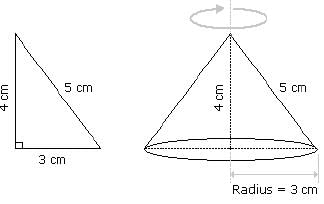
A right triangle with sides 3 cm, 4 cm and 5 cm is rotated the side of 3 cm to form a cone. The volume of the cone so formed is:
In a shower, 5 cm of rain falls. The volume of water that falls on 1.5 hectares of ground is:
A hall is 15 m long and 12 m broad. If the sum of the areas of the floor and the ceiling is equal to the sum of the areas of four walls, the volume of the hall is:
66 cubic centimetres of silver is drawn into a wire 1 mm in diameter. The length of the wire in metres will be:
A hollow iron pipe is 21 cm long and its external diameter is 8 cm. If the thickness of the pipe is 1 cm and iron weighs 8 g/cm3, then the weight of the pipe is:
A boat having a length 3 m and breadth 2 m is floating on a lake. The boat sinks by 1 cm when a man gets on it. The mass of the man is:
50 men took a dip in a water tank 40 m long and 20 m broad on a religious day. If the average displacement of water by a man is 4 m3, then the rise in the water level in the tank will be:
The slant height of a right circular cone is 10 m and its height is 8 m. Find the area of its curved surface.
A cistern 6m long and 4 m wide contains water up to a depth of 1 m 25 cm. The total area of the wet surface is:
A metallic sheet is of rectangular shape with dimensions 48 m x 36 m. From each of its corners, a square is cut off so as to make an open box. If the length of the square is 8 m, the volume of the box (in m3) is:
The curved surface area of a cylindrical pillar is 264 m2 and its volume is 924 m3. Find the ratio of its diameter to its height.
A cistern of capacity 8000 litres measures externally 3.3 m by 2.6 m by 1.1 m and its walls are 5 cm thick. The thickness of the bottom is:
What is the total surface area of a right circular cone of height 14 cm and base radius 7 cm?
A large cube is formed from the material obtained by melting three smaller cubes of 3, 4 and 5 cm side. What is the ratio of the total surface areas of the smaller cubes and the large cube?
How many bricks, each measuring 25 cm × 11.25 cm × 6 cm, will be needed to build a wall of 8 m × 6 m × 22.5 cm?
What is the volume of 32 metre high cylindrical tank?
I. The area of its base is 154 m2.
II. The diameter of the base is 14 m.
Is a given rectangular block a cube?
I. At least 2 faces of the rectangular block are squares.
II. The volume of the block is 64.
What is the capacity of a cylindrical tank?
I. Radius of the base is half of its height which is 28 metres.
II. Area of the base is 616 sq. metres and its height is 28 metres.
What is the height of a circular cone?
I. The area of that cone is equal to the area of a rectangle whose length is 33 cm.
II. The area of the base of that cone is 154 sq. cm.
What is the volume of a cube?
I. The area of each face of the cube is 64 square metres.
II. The length of one side of the cube is 8 metres.