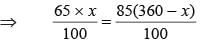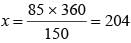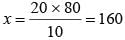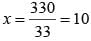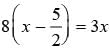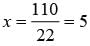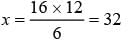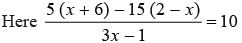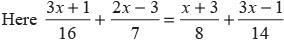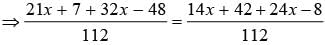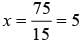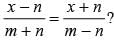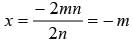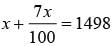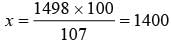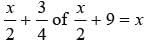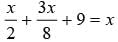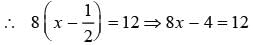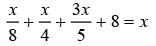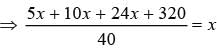All Courses
Get the App Signup / Login
Sign in Open App
Class 8 Exam  >  Class 8 Tests  >  Mathematical Olympiad Class 8  >  Olympiad Test: Linear Equations In One Variable - Class 8 MCQ

Olympiad Test: Linear Equations In One Variable - Class 8 MCQ


Test Description

20 Questions MCQ Test Mathematical Olympiad Class 8 - Olympiad Test: Linear Equations In One Variable

Olympiad Test: Linear Equations In One Variable for Class 8 2024 is part of Mathematical Olympiad Class 8 preparation. The Olympiad Test: Linear Equations In One Variable questions and answers have been prepared according to the Class 8 exam syllabus.The Olympiad Test: Linear Equations In One Variable MCQs are made for Class 8 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Olympiad Test: Linear Equations In One Variable below.
Solutions of Olympiad Test: Linear Equations In One Variable questions in English are available as part of our Mathematical Olympiad Class 8 for Class 8 & Olympiad Test: Linear Equations In One Variable solutions in Hindi for Mathematical Olympiad Class 8 course. Download more important topics, notes, lectures and mock test series for Class 8 Exam by signing up for free. Attempt Olympiad Test: Linear Equations In One Variable | 20 questions in 40 minutes | Mock test for Class 8 preparation | Free important questions MCQ to study Mathematical Olympiad Class 8 for Class 8 Exam | Download free PDF with solutions
Olympiad Test: Linear Equations In One Variable - Question 1
Save

A boat goes downstream and covers the distance between two ports in 4 hours, while it covers the same distance upstream in 5 hours. If the speed of the stream is 2km/hour. what is the speed of boat in still water ?

Detailed Solution for Olympiad Test: Linear Equations In One Variable - Question 1

Let the speed of boat in still water be x km/hour. 
∴ (x + 2) 4 = (x – 2) 5
⇒  4x + 8 = 5x - 10
⇒ x = 18 km/hr

Olympiad Test: Linear Equations In One Variable - Question 2
Save

The ages of Mohan and Sohan are in the ratio 9 : 7. Ten years ago their ages were in the ratio 7 : 5. What is the difference between their present ages?

Detailed Solution for Olympiad Test: Linear Equations In One Variable - Question 2

Let Mohan’s age = 9x
and Sohan’s age = 7x
10, years ago,
Mohan’s age = 9x – 10
Sohan’s age = 7x – 10

⇒ 45x – 50 = 49x – 70
⇒ 4x = 20 ⇒ x = 5
∴ Mohan’s age = 9 × 5 = 45
and Sohan’s age = 7 × 5 = 35
Hence difference = 45 – 35 = 10 years

1 Crore+ students have signed up on EduRev. Have you? Download the App
Olympiad Test: Linear Equations In One Variable - Question 3
Save

The sum of two numbers is 360. If 65% of one number is equal to 85% of the other. What is the largest number among them?

Detailed Solution for Olympiad Test: Linear Equations In One Variable - Question 3

Let the one number be x.
Other number = 360 – x
Now 65% of x = 85% of (360 – x)

⇒ 65 x + 85x = 85 × 360
⇒ 150x = 85 × 360
⇒ 

Olympiad Test: Linear Equations In One Variable - Question 4
Save

A certain number of workers can finish a piece of work in 70 days. If there are 20 men less, it would take 10 days more for the same work to be finished. How many workers were there in starting?
Detailed Solution for Olympiad Test: Linear Equations In One Variable - Question 4

Let the no. of workers in starting be x.
∴ 70 × x = (x – 20) 80
⇒ 70 x = 80x – 20 × 80
⇒ 10x = 20 × 80
⇒ 

Olympiad Test: Linear Equations In One Variable - Question 5
Save

The sum of three consecutive multiples of 11 is 363. Which of these multiple is greatest?
Detailed Solution for Olympiad Test: Linear Equations In One Variable - Question 5

Let the numbers be
11x, 11(x + 1), 11(x + 2)
Hence 11x + 11(x + 1) + 11(x + 2) = 363
⇒ 11x + 11x + 11 + 11x + 22 = 363
⇒ 33x + 33 = 363
⇒ 
Greatest multiple = 11(x + 2)
= 11 (10 + 2) = 11 × 12 = 132

Olympiad Test: Linear Equations In One Variable - Question 6
Save

Arun’s age is three times his son’s age. 10 years age he was 5 times his son’s age. What is the sum of their present ages?
Detailed Solution for Olympiad Test: Linear Equations In One Variable - Question 6

Let Son’s age = x years
∴ Arun’s age = 3x.
Now 10 years ago, son’s age = x – 10.
Given Arun’s age = 3x – 10
⇒ 3x -10 = 5 (x – 10)
⇒ 3x – 10 = 5x – 50
2x = 40 ⇒ x = 20 years
Arun’s  age = 3 × 20 = 60 years
Sum of Arun’s and Son’s age = 20 + 60
= 80 years

Olympiad Test: Linear Equations In One Variable - Question 7
Save

Nirmal thinks of a number and subtracts 5/2 from it. He multiplies the result by 8. The result now obtained is 3 times the same number he thought of. Find the number.
Detailed Solution for Olympiad Test: Linear Equations In One Variable - Question 7

Let the number be x.

⇒ 8x - 20 = 3x
⇒ 5x = 20
⇒ x = 4

Olympiad Test: Linear Equations In One Variable - Question 8
Save

The difference between the digits of a two-digit number is 3. If the digits are interchanged and the resulting number is added to the original number we get 143. What was the original number?
Detailed Solution for Olympiad Test: Linear Equations In One Variable - Question 8

Let the unit’s digit be x.
Ten’s digit = x + 3.Original number =10(x + 3) + 1(x)
= 10x + 30 + x
= 11x + 30
After interchange, resulting number
= 10 (x) + 1 (x + 3)
= 10x + x + 3
= 11x + 3
∴ 11x + 3 + 11x + 30 = 143
⇒ 22x + 33 = 143
⇒ 22x = 143 – 33
⇒ 22x = 110
⇒ 
Original number = 11x + 3 = 11 × 5 + 3
= 55 + 3 = 58

Olympiad Test: Linear Equations In One Variable - Question 9
Save

A grand father is ten times older than his grandson. He is then also 54 years older than him. What is the difference of their present ages?
Detailed Solution for Olympiad Test: Linear Equations In One Variable - Question 9

 Let the age of grand son be x years.
Grand father’s age = 10x.
⇒ 10x = 54 + x
⇒ 9x = 54
⇒ x = 6
Grand father’s age = 10 × 6 = 60 years
Difference of their present ages = 60 – 6 = 54.

Olympiad Test: Linear Equations In One Variable - Question 10
Save

An altitude of a triangle is five-thirds the length of its corresponding base. If the altitude is increased by 4 cm and the base is decreased by 2 cm, but the area of triangle remains the same. Find the base and altitude of the triangle respectively.
Detailed Solution for Olympiad Test: Linear Equations In One Variable - Question 10

Initial Area of the Triangle

The area of the triangle is calculated as:

Area = 12 × b × 53 b = 56 b²

New Area with Changes

Now, with the new base and altitude, the area becomes:

New Area = 12 × (b - 2) × ( 53 b + 4 )

Setting the New Area Equal to the Original

We equate the new area to the original area:

(b - 2) × ( 53 b + 4) = 53 b²

Simplification

After simplifying, we solve for b:

12b - 10b - 24 = 0
2b = 24
b = 12 cm

Finding the Altitude

The altitude is:

Altitude = 53 × 12 = 20 cm

Final Answer: The base is 12 cm and the altitude is 20 cm.

Olympiad Test: Linear Equations In One Variable - Question 11
Save

A field can be ploughed in 18 days. If everyday an additional area of 16 hectares is ploughed, the field can be ploughed in 12 days. What is the area of the field?
Detailed Solution for Olympiad Test: Linear Equations In One Variable - Question 11

Let the area of the field ploughed daily be x hectares.
Area of the field = 18x
⇒ 18x = (x + 16) 12
⇒ 18x = 12x + 16 × 12
⇒ 6x = 16 × 12
⇒ 
​Area of the field = 18 × 32 = 576 hectares

Olympiad Test: Linear Equations In One Variable - Question 12
Save

The sum of the digits of a two number is 9. If 9 is subtracted from the number its digits are interchanged. What is the number?
Detailed Solution for Olympiad Test: Linear Equations In One Variable - Question 12

Let the unit’s digit be x.
Ten’s digit = 9 – x
Number = 10 (9 – x) + 1(x)
= 90 – 10x + x= 90 – 9x
90 – 9x – 9 = x(10) + 1(9 – x)
⇒ 81 – 9x = 10x + 9 – x
⇒ 81 – 9x = 9x + 9
⇒ 18x = 72 ⇒ x = 4
Number = 90 – 9 × 4 = 90 – 36 = 54

Olympiad Test: Linear Equations In One Variable - Question 13
Save

What is the value of x in the given equatiom?
Detailed Solution for Olympiad Test: Linear Equations In One Variable - Question 13


⇒ 5x + 30 – 30 + 15x = 30x – 10
⇒ 20x + 10 = 30x
⇒ 10x = 10 ⇒ x = 1

Olympiad Test: Linear Equations In One Variable - Question 14
Save

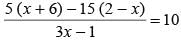
 What is the value of x in the given equation
Detailed Solution for Olympiad Test: Linear Equations In One Variable - Question 14



⇒ 53x - 41 = 38x + 34
⇒ 15x = 34 + 41
⇒ 

Olympiad Test: Linear Equations In One Variable - Question 15
Save

What is the value of x if
Detailed Solution for Olympiad Test: Linear Equations In One Variable - Question 15

⇒ (x – n) (m – n) = (x + n)(m + n)
⇒ mx – mn – nx + n2 = mx + mn + nx + n2
⇒ - mn – nx = mn + nx
⇒ 2nx = -2mn
⇒ 

Olympiad Test: Linear Equations In One Variable - Question 16
Save

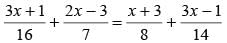
A shirt is sold for Rs. 1498 and the seller gains 7% on it. What is the cost price of the shirt ?
Detailed Solution for Olympiad Test: Linear Equations In One Variable - Question 16

Let the cost price of the shirt be Rs. x.
∴ x + 7% of x = 1498
⇒ 
⇒ 107x 1498 x 100
⇒ 

Olympiad Test: Linear Equations In One Variable - Question 17
Save

Half of a herd of deer are grazing in the field and three fourth of remaining are playing nearby. The rest nine are drinking water from the river. What is the number of deer in the herd?
Detailed Solution for Olympiad Test: Linear Equations In One Variable - Question 17

Let number of deer be x.
∴ 
⇒ 
⇒ 4x + 3x 72 = 8x
⇒  x = 72 

Olympiad Test: Linear Equations In One Variable - Question 18
Save

The ages of Raju and Rajan are in the ratio 5 : 8. If Raju was 5 years older and Rajan 4 years younger, the age of Raju would have been the same as the age of Rajan. What is the age of Raju?
Detailed Solution for Olympiad Test: Linear Equations In One Variable - Question 18

Let Raju’s age = 5x.
∴ Rajan ‘s age = 8x
∴ 5x + 5 = 8x – 4
⇒ 3x = 9 ⇒ x = 3
Raju’s age = 5 × = 15 years

Olympiad Test: Linear Equations In One Variable - Question 19
Save

If 1/2 is subtracted from a number and the difference is multiplied by 8, the result is 12. What is the number?
Detailed Solution for Olympiad Test: Linear Equations In One Variable - Question 19

Let the number be x.

⇒ 8x = 16
⇒ x = 2

Olympiad Test: Linear Equations In One Variable - Question 20
Save

Mohaesh travelled 1/8 th of his Journey by bus, 1/4 th by taxi, 3/5 th by train and remaining 8 km by foot. What is the length of his total Journey?​
Detailed Solution for Olympiad Test: Linear Equations In One Variable - Question 20

Let length of total Journey be x km.


⇒ 39x + 320 = 40x
⇒ x = 320

28 videos|52 docs|63 tests
Join Course
Information about Olympiad Test: Linear Equations In One Variable Page
In this test you can find the Exam questions for Olympiad Test: Linear Equations In One Variable solved & explained in the simplest way possible. Besides giving Questions and answers for Olympiad Test: Linear Equations In One Variable, EduRev gives you an ample number of Online tests for practice

Top Courses for Class 8

28 videos|52 docs|63 tests
Join Course
Download as PDF

Top Courses for Class 8

Important Questions for Olympiad Test: Linear Equations In One Variable

Find all the important questions for Olympiad Test: Linear Equations In One Variable at EduRev.Get fully prepared for Olympiad Test: Linear Equations In One Variable with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the Olympiad Test: Linear Equations In One Variable syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of Olympiad Test: Linear Equations In One Variable resources.

Olympiad Test: Linear Equations In One Variable MCQs with Answers

Prepare for the Olympiad Test: Linear Equations In One Variable within the Class 8 exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for Olympiad Test: Linear Equations In One Variable Mathematical Olympiad Class 8

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace Olympiad Test: Linear Equations In One Variable with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Follow Us
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup