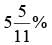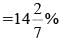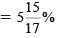Olympiad Test: Profit And Loss - 1 - Class 7 MCQ
20 Questions MCQ Test Mathematics Olympiad Class 7 - Olympiad Test: Profit And Loss - 1
Alfred buys an old scooter for Rs 4700 and spends Rs 800 on its repairs. If he sells the scooter for Rs 5800, his gain percent is:
The cost price of 20 articles is the same as the selling price of x articles. If the profit is 25%, then the value of x is:
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If selling price is doubled, the profit triples. Find the profit percent.
In a certain store, the profit is 320% of the cost. If the cost increases by 25% but the selling price remains constant, approximately what percentage of the selling price is the profit?
A vendor bought toffees at 6 for a rupee. How many for a rupee must he sell to gain 20%?
The percentage profit earned by selling an article for Rs 1920 is equal to the percentage loss incurred by selling the same article for Rs 1280. At what price should the article be sold to make 25% profit?
A shopkeeper expects a gain of 22.5% on his cost price. If in a week, his sale was of Rs 392, what was his profit?
A man buys a cycle for Rs 1400 and sells it at a loss of 15%. What is the selling price of the cycle?
Sam purchased 20 dozens of toys at the rate of Rs 375 per dozen. He sold each one of them at the rate of Rs 33. What was his percentage profit?
Some articles were bought at 6 articles for Rs 5 and sold at 5 articles for Rs 6. Gain percent is:
On selling 17 balls at Rs 720, there is a loss equal to the cost price of 5 balls. The cost price of a ball is:
When a plot is sold for Rs 18,700, the owner loses 15%. At what price must that plot be sold in order to gain 15%?
100 oranges are bought at the rate of Rs 350 and sold at the rate of Rs 48 per dozen. The percentage of profit or loss is:
A shopkeeper sells one transistor for Rs 840 at a gain of 20% and another for Rs 960 at a loss of 4%. His total gain or loss percent is:
A trader mixes 26 kg of rice at Rs 20 per kg with 30 kg of rice of other variety at Rs 36 per kg and sells the mixture at Rs 30 per kg. His profit percent is:
A shopkeeper sells some articles at the profit of 25% on the original price. What is the exact amount of profit? To find the answer, which of the following information given in statementsI and II is/are necessary?
I. Sale price of the article
II. Number of articles sold
A shopkeeper sells some toys at Rs 250 each. What percent profit does he make? To find the answer, which of the following information given in statements I and II is/are necessary?
I. Number of toys sold
II. Cost price of each toy
A man mixes two types of rice (X and Y) and sells the mixture at the rate of Rs 17 per kg. Find his profit percentage.
I. The rate of X is Rs 20 per kg
II. The rate of Y is Rs 13 per kg
By selling a product with 20% profit, how much profit was earned?
I. The difference between cost and selling price is Rs 40.
II. The selling price is 120 percent of the cost price.
By selling an article what is the profit percent gained?
I. 5% discount is given on list price.
II. If discount is not given, 20% profit is gained.
III. The cost price of the articles is Rs 5000.
|
24 videos|57 docs|102 tests
|
|
24 videos|57 docs|102 tests
|
Top Courses for Class 7
Important Questions for Olympiad Test: Profit And Loss - 1
Olympiad Test: Profit And Loss - 1 MCQs with Answers
Online Tests for Olympiad Test: Profit And Loss - 1 Mathematics Olympiad Class 7
|
© EduRev
|
Education Revolution
|
|
