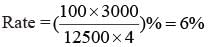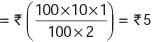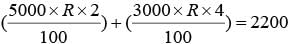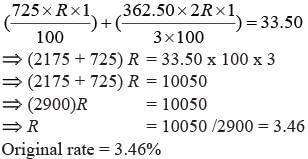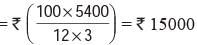All Courses
Get the App Signup / Login
Sign in Open App
Class 7 Exam  >  Class 7 Tests  >  Mathematics Olympiad Class 7  >  Olympiad Test: Simple Interest - 1 - Class 7 MCQ

Olympiad Test: Simple Interest - 1 - Class 7 MCQ


Test Description

20 Questions MCQ Test Mathematics Olympiad Class 7 - Olympiad Test: Simple Interest - 1

Olympiad Test: Simple Interest - 1 for Class 7 2024 is part of Mathematics Olympiad Class 7 preparation. The Olympiad Test: Simple Interest - 1 questions and answers have been prepared according to the Class 7 exam syllabus.The Olympiad Test: Simple Interest - 1 MCQs are made for Class 7 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Olympiad Test: Simple Interest - 1 below.
Solutions of Olympiad Test: Simple Interest - 1 questions in English are available as part of our Mathematics Olympiad Class 7 for Class 7 & Olympiad Test: Simple Interest - 1 solutions in Hindi for Mathematics Olympiad Class 7 course. Download more important topics, notes, lectures and mock test series for Class 7 Exam by signing up for free. Attempt Olympiad Test: Simple Interest - 1 | 20 questions in 40 minutes | Mock test for Class 7 preparation | Free important questions MCQ to study Mathematics Olympiad Class 7 for Class 7 Exam | Download free PDF with solutions
Olympiad Test: Simple Interest - 1 - Question 1
Save

A person borrows Rs 5000 for 2 years at 4% p.a. simple interest. He immediately lends it to another person at 6.25% p.a. for 2 years. Find his gain in the transaction per year.

Detailed Solution for Olympiad Test: Simple Interest - 1 - Question 1

Gain in 2 years
= Rs [(5000 × 25/4 × 2/100)
– {(5000 × 4 × 2)/100}]
= Rs (6 25 – 400)
= Rs 225
Gain in 1 year = Rs 225/2 =112.50

Olympiad Test: Simple Interest - 1 - Question 2
Save

A certain amount earns simple interest of Rs 1750 after 7 years. Had the interest been 2% more, how much more interest would it have earned?

Detailed Solution for Olympiad Test: Simple Interest - 1 - Question 2

We need to know the S.I., principal and time to find the rate.
Since the principal is not given, so data is inadequate.

1 Crore+ students have signed up on EduRev. Have you? Download the App
Olympiad Test: Simple Interest - 1 - Question 3
Save

What will be the ratio of simple interest earned by certain amount at the same rate of interest for 6 years and that for 9 years?

Detailed Solution for Olympiad Test: Simple Interest - 1 - Question 3

Let the principal be P and rate of interest be R%.
Required ratio

Olympiad Test: Simple Interest - 1 - Question 4
Save

A sum of Rs 12,500 amounts to Rs 15,500 in 4 years at the rate of simple interest. What is the rate of interest?
Detailed Solution for Olympiad Test: Simple Interest - 1 - Question 4

S.I. = Rs (15500 – 12500) = Rs 3000

Olympiad Test: Simple Interest - 1 - Question 5
Save

An automobile financier claims to be lending money at simple interest, but he includes the interest every six months for calculating the principal. If he is charging an interest of 10%, the effective rate of interest becomes:
Detailed Solution for Olympiad Test: Simple Interest - 1 - Question 5

Let the sum be Rs 100. Then,
S.I. for first 6 months

S.I. for last 6 months

So, amount at the end of 1 year
= Rs (100 + 5 + 5.25) = Rs 110.25
Effective rate = (110.25 – 100) = 10.25%

Olympiad Test: Simple Interest - 1 - Question 6
Save

A lent Rs 5000 to B for 2 years and Rs 3000 to C for 4 years on simple interest at the same rate of interest and received Rs 2200 in all from both of them as interest. The rate of interest per annum is:
Detailed Solution for Olympiad Test: Simple Interest - 1 - Question 6

Let the rate be R% p.a.
Then,

⇒ 100R + 120R = 2200
⇒ R = 2200/220
Rate = 10%.

Olympiad Test: Simple Interest - 1 - Question 7
Save

A sum of Rs 725 is lent in the beginning of a year at a certain rate of interest. After 8 months, a sum of Rs 362.50 more is lent but at the rate twice the former. At the end of the year, Rs 33.50 is earned as interest from both the loans. What was the original rate of interest?
Detailed Solution for Olympiad Test: Simple Interest - 1 - Question 7

Let the original rate be R%. Then, new rate = (2R) %.
Note: Here, original rate is for 1 year(s);
the new rate is for only 4 months i.e. 1/3 year(s).

Olympiad Test: Simple Interest - 1 - Question 8
Save

A man took loan from a bank at the rate of 12% p.a. simple interest. After 3 years he had to pay Rs 5400 interest only for the period. The principal amount borrowed by him was:
Detailed Solution for Olympiad Test: Simple Interest - 1 - Question 8

Principal 

Olympiad Test: Simple Interest - 1 - Question 9
Save

A sum of money amounts to Rs 9800 after 5 years and Rs 12005 after 8 years at the same rate of simple interest. The rate of interest per annum is:
Detailed Solution for Olympiad Test: Simple Interest - 1 - Question 9

S.I. for 3 years = Rs (12005 – 9800)
= Rs 2205

Principal = Rs (9800 – 3675) = Rs 6125
Hence, rate = (100 × 3675)/(6125 × 5) = 12% 

Olympiad Test: Simple Interest - 1 - Question 10
Save

A sum of money at simple interest amounts to Rs 815 in 3 years and to ` 854 in 4 years. The sum is:
Detailed Solution for Olympiad Test: Simple Interest - 1 - Question 10

S.I. for 1 year = Rs (854 – 815) = Rs 39
S.I. for 3 years = Rs (39 × 3) = Rs 117
∴ Principal = Rs (815 – 117) = Rs 698

Olympiad Test: Simple Interest - 1 - Question 11
Save

Mr. Thomas invested an amount of Rs 13,900 divided in two different schemes A and B at the simple interest rate of 14% p.a. and 11% p.a. respectively. If the total amount of simple interest earned in 2 years be ` 3508, what was the amount invested in Scheme B?
Detailed Solution for Olympiad Test: Simple Interest - 1 - Question 11

Let the sum invested in Scheme A be Rs x and that in Scheme B be Rs (13900 – x).
Then,

= 3508
⇒ 28x – 22x = 350800 – (13900 × 22)
⇒ 6x = 45000
⇒ x = 7500
So, sum invested in Scheme B
= Rs (13900 – 7500) = Rs 6400

Olympiad Test: Simple Interest - 1 - Question 12
Save

A sum fetched a total simple interest of Rs 4016.25 at the rate of 9% p.a. in 5 years. What is the sum?
Detailed Solution for Olympiad Test: Simple Interest - 1 - Question 12

Principal = Rs (100 × 4016.25)/(9 × 5)
= Rs 401625/45
= Rs 8925

Olympiad Test: Simple Interest - 1 - Question 13
Save

How much time will it take for an amount of Rs 450 to yield Rs 81 as interest at 4.5% per annum of simple interest?
Detailed Solution for Olympiad Test: Simple Interest - 1 - Question 13

Time = (100 × 81)/ (450 × 4.5) years
= 4 years

Olympiad Test: Simple Interest - 1 - Question 14
Save

Reena took a loan of  Rs 1200 with simple interest for as many years as the rate of interest. If she paid Rs 432 as interest at the end of the loan period, what was the rate of interest?​
Detailed Solution for Olympiad Test: Simple Interest - 1 - Question 14

Let rate = R% and time = R years.
Then,(1200 × R × R)/100 = 432
⇒ 12R2 = 432
⇒ R2 = 36
⇒ R = 6

Olympiad Test: Simple Interest - 1 - Question 15
Save

Anita borrowed Rs 800 for 2 years at the rate of 12% per annum. Find the interest. Also find the amount paid by her.
Detailed Solution for Olympiad Test: Simple Interest - 1 - Question 15

Principal = ‘P’ = Rs 800, Rate = R
= 12% = 0.12, Time= ‘T’ = 2 years.
Interest: I = P × R × T I = 800 × 0.12 × 2
I = 192
Amount: A = P + I
A = 800 + 192 = Rs 992

Olympiad Test: Simple Interest - 1 - Question 16
Save

Deepak takes a loan of Rs 8,000 to buy a used truck at the rate of 9 % simple interest. Calculate the annual interest to be paid for the loan amount.
Detailed Solution for Olympiad Test: Simple Interest - 1 - Question 16

From the details given in the problem
Principal = P = Rs 8,000 and R = 9 %
or 0.09 expressed as a decimal.
As the annual interest is to be calculated, the time period T =1.
Plugging these values in the simple interest formula, I = P × T × R
= 8,000 × 1 × 0.09
= 720.00
Annual interest to be paid = Rs 720

Olympiad Test: Simple Interest - 1 - Question 17
Save

Steve invested $ 10,000 in a savings bank account that earned 2% simple interest. Find the interest earned if the amount was kept in the bank for 4 years.
Detailed Solution for Olympiad Test: Simple Interest - 1 - Question 17

Principal P = $ 10,000, Time Period T = 4
years and Rate of Interest = 2% = 0.02
Plugging these values in the simple
Interest formula,
I = P × T × R
= 10,000 × 4 × 0.02
= $ 800
Interest earned for the investment = $ 800

Olympiad Test: Simple Interest - 1 - Question 18
Save

Ryan bought $ 15,000 from a bank to buy a car at 10% simple interest. If he paid $ 9,000 as interest while clearing the loan, find the time for which the loan was given.
Detailed Solution for Olympiad Test: Simple Interest - 1 - Question 18

Principal = $ 15,000, Rate of Interest R = 10% = 0.10 and the Interest paid = I = $ 9,000. And T is to be found.
T = I/(PR)
= 9000/(15,000 × 0.10)
= 6 years.
The loan was given for 6 years.

Olympiad Test: Simple Interest - 1 - Question 19
Save

In how much time will the simple interest on $3,500 at the rate of 9% p.a be the same as simple interest on $4,000 at 10.5% p.a for 4 years?
Detailed Solution for Olympiad Test: Simple Interest - 1 - Question 19

S.I on $4,000 at rate 10.5% = 10.5/100
= 0.105 for 4 years
S.I  = (P × R × T) /100
= 4000 × 0.105 × 4
S.I = $ 1,680
The interest of $1,680 is the same as that on $3,500 at 9% p.a. for supposed years.
Time = t = (S.I × 100)/(P × R )
= (1680 × 100)/ (3500 × 9)
Time = t = 5.33 years.

Olympiad Test: Simple Interest - 1 - Question 20
Save

In what time will Rs 8500 amount to Rs 15767.50 at 4.5% per annum?
Detailed Solution for Olympiad Test: Simple Interest - 1 - Question 20

Here interest = Rs 15767.50 – 8500   =Rs 7267.50
Therefore t =  (7267.50 × 100)/(8500 ×4.5) = 19 years

24 videos|57 docs|100 tests
Join Course
Information about Olympiad Test: Simple Interest - 1 Page
In this test you can find the Exam questions for Olympiad Test: Simple Interest - 1 solved & explained in the simplest way possible. Besides giving Questions and answers for Olympiad Test: Simple Interest - 1, EduRev gives you an ample number of Online tests for practice

Top Courses for Class 7

24 videos|57 docs|100 tests
Join Course
Download as PDF

Top Courses for Class 7

Important Questions for Olympiad Test: Simple Interest - 1

Find all the important questions for Olympiad Test: Simple Interest - 1 at EduRev.Get fully prepared for Olympiad Test: Simple Interest - 1 with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the Olympiad Test: Simple Interest - 1 syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of Olympiad Test: Simple Interest - 1 resources.

Olympiad Test: Simple Interest - 1 MCQs with Answers

Prepare for the Olympiad Test: Simple Interest - 1 within the Class 7 exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for Olympiad Test: Simple Interest - 1 Mathematics Olympiad Class 7

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace Olympiad Test: Simple Interest - 1 with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup