Olympiad Test: Understanding Quadrilaterals - Grade 8 MCQ
20 Questions MCQ Test - Olympiad Test: Understanding Quadrilaterals
ABCD is a quadrilateral. If AC and BD bisect each other, what ABCD can be?
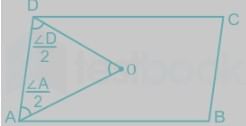
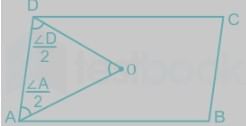
ABCD is a parallelogram. The angle bisectors of ∠A and ∠D meet at O. What is the measure of ∠AOD?

The diagonal of a rectangle is 10 cm and its breadth is6 cm. What is its length?
ABCD and MNOP are quadrilaterals as shown in the figure.
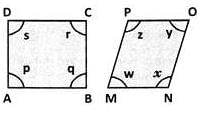
Which of the following is correct?
What do you call a parallelogram which has equal diagonals?
In a square ABCD, the diagonals bisect at O. What type of a triangle is AOB?
The perimeter of a parallelogram is180 cm. If one side exceeds the other by 10 cm, what are the sides of the parallelogram?
In the quadrilateral ABCD, the diagonals AC and BD are equal and perpendicular to each other. What type of a quadrilateral is ABCD?
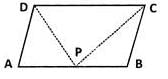
ABCD is a parallelogram as shown in the figure. If AB = 2AD and P is the mid-point of AB, what is the measure of ∠CPD ?
In a parallelogram ABCD, if AB = 2x+5, CD = y+1, AD= y+5 and BC = 3x−4,what is the ratio of AB and BC?
If ABCD is an isosceles trapezium, what is the measure of ∠C?
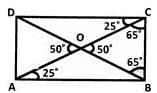
A diagonal of a rectangle is inclined to one side of the rectangle at 25o. What is the measure of the acute angle between the diagonals?
If angles P, Q, R and S of the quadrilateral PQRS, taken in order, are in the ratio 3:7:6:4, what is PQRS?
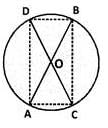
If AB and CD are diameters, what is ACBD?
If two adjacent angles of a parallelogram are in the ratio 3:2, what are their measures?
ABC and DEF are straight lines.
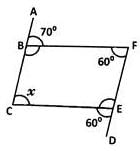
Find the value of 'x',
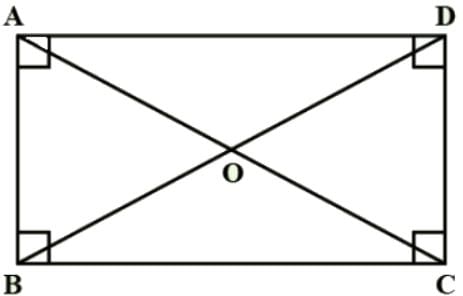
ABCD is a rectangle. Its diagonals meet at O.
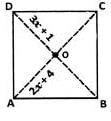
Find x; if OA = 2x+4 and OD = 3x+1.
ABCD is a rhombus with diagonals intersecting at O.
In the given figure,
OC =12, OD =5, AB =13
OB = x, OA = y, and the side of the rhombus is z. Given the lengths marked in the figure, find the respective values of x, y, and z.
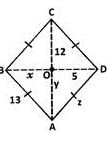
Find the respective values of x, y and z.
In the figure, ABCD is a parallelogram.
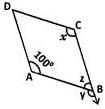
Find the respective values of x, y and z.
In the figure, ABCD is a rhombus and ABDE is a parallelogram.
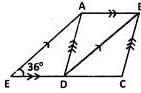
Given that EDC is a straight line and ∠AED = 36o find ∠BAD.