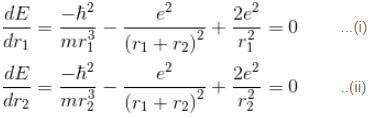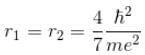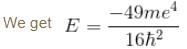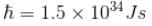Origin Of Quantum Mechanics NAT Level – 2 - Physics MCQ
10 Questions MCQ Test - Origin Of Quantum Mechanics NAT Level – 2
The life time of a nucleus in excited state is 10–12s. The uncertainty in the energy and frequency of γ-ray photon emitted by it. (h = 6.63 × 10–34 Js) (in units of 1011 Hz) is a × 1011Hz. Find a.
The number of photon emitted per second by a 40W source of mono chromatic light of wavelength 6000Å is given by x × 1020. Find the value of x.
For what wavelength of photon does compton scattering result in a photon whose energy is one half that of the original photon at a scattering angle of 45º? Give the answer as [a × 10–3 Å] . Find the value of a.
For what value of an electron’s speed will its de-Broglie wavelength be same as the compton wavelength? (in terms of c)
Gamma ray photons of energy 1.02 MeV are scattered from electrons which are initially at rest. Find the angle for symmetric scattering at this energy (in degrees)
The average life time of an excited atomic state is 10–8s. If the wavelength of the spectral line associated with the transition from this state to the ground state is 6000 Å. What will be the width of this line? (in femtometer)
If the X-ray photon is scattered at angle of 180° and electron recoils with an energy of 4 keV. Then calculate the wavelength of the incident photon (in Å) in angstroms.
The minimum kinetic energy of an alpha particle that can exist in a nucleus (use uncertainty principle 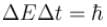 ) (Radius of nucleus = 10–14m) (in keV)
) (Radius of nucleus = 10–14m) (in keV)
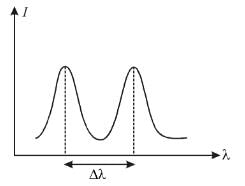
The intensity of scattered monochromatic beam of X-rays is plotted as a function of wavelength. There are 2 peaks observed. The distance between the 2 peaks is 0.024 Å. Find the angle (in degrees) at which the X-rays are scattered.
Calculate the ground state energy of a Helium atom, using the uncertainty principle. (in eV)


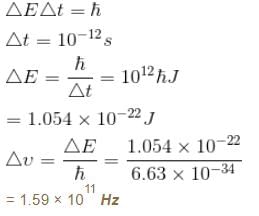

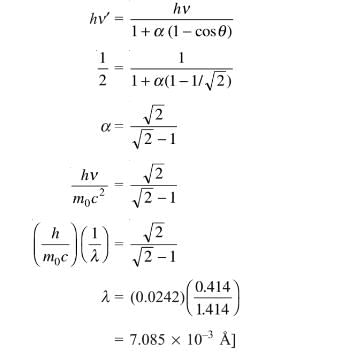
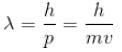
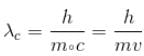
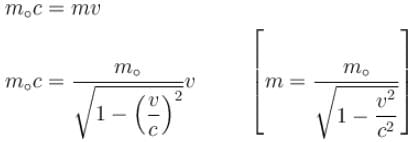
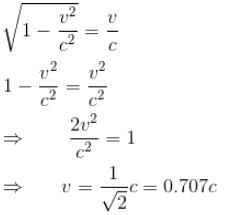
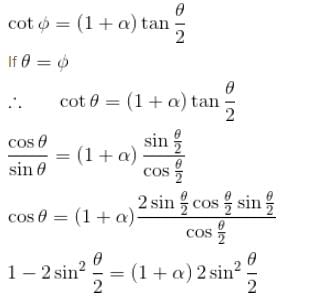
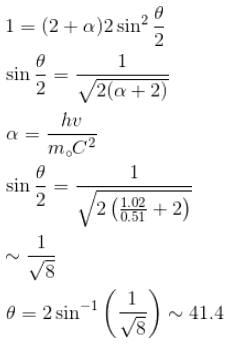
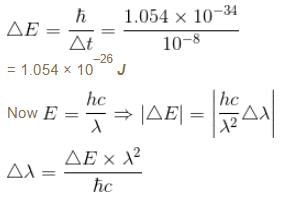
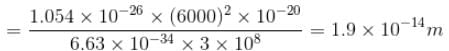
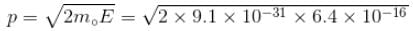
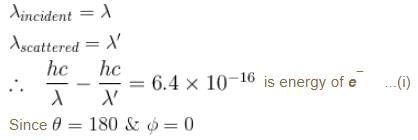
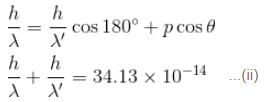
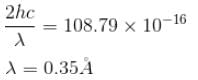

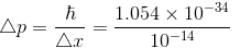

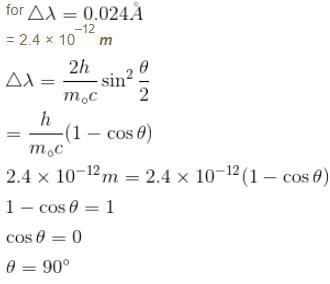
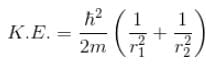
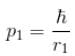

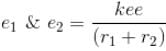
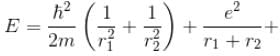 Interaction between nucleus and electron
Interaction between nucleus and electron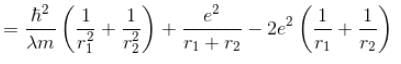
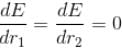 since in the ground state, Energy is minimum.
since in the ground state, Energy is minimum.