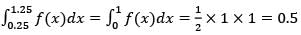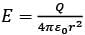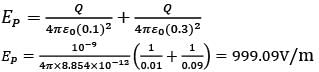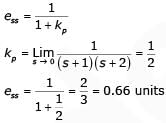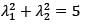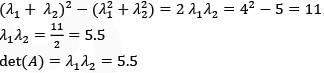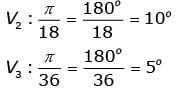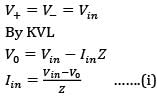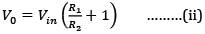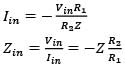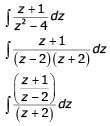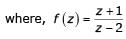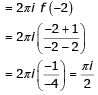Past Year Paper 2018 ( Electrical Engineering) - Electrical Engineering (EE) MCQ
30 Questions MCQ Test - Past Year Paper 2018 ( Electrical Engineering)
For what values of k given below is 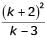 an integer?
an integer?
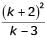 an integer?
an integer?“Since you have gone off the _________, the _________ sand is likely to damage the car”. The words that best fill the blanks in the above sentence are
The three roots of the equation f (x ) = 0 are x = {-2, 0, 3}. What are the three values of for which f (x - 3)= 0 ?
Functions, F ( a, b) and G ( a, b) are defined as follows:
F (a, b) = ( a− b)2 and G ( a, b) = |a− b|, where |x| represents the absolute value of x. What would be the value of G ( F (1, 3) , G (1, 3)) ?
“A common misconception among writers is that sentence structure mirrors thought; the more _________ the structure, the ted the ideas”.
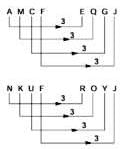
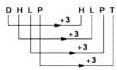
In a certain code AMCF is written as EQGJ and NKUF is written as ROYJ. How will DHLP be written in the code?
An e-mail password must contain three characters. The password has to contain one numeral from 0 to 9, one upper case and one lower case character from the English alphabet. How many distinct passwords are possible?
A designer uses marbles of four different colours of his designs. The cost of each marble is the same, irrespective of the colour. The table below shows the percentage of marbles of each colour used in the current design. The cost of each marble increased by 25%. Therefore, the designer decided to reduce equal numbers of marbles of each colour to keep the total cost unchanged. What is the percentage of blue marbles in the new design?

P, Q, R and S crossed a lake in a boat that can hold a maximum of two persons, with only one set of oars. The following additional facts are available
i. The boat held two persons on each of the three forward trips across lake and one person on each of the two return trips.
ii. P is unable to row when someone else is in the boat.
iii. Q is unable to row with anyone else except R.
iv. Each person rowed for at least one trip.
v. Only one person can row during a trip.
Who rowed twice?
A class of twelve children has two more boys than girls. A group of three children are randomly picked from this class to accompany the teacher on a field trip. What is the probability that the group accompanying the teacher contains more girls than boys?
Match the transfer functions of the second-order systems with the nature of the system given below.

Consider a lossy transmission line with V1 and V2 as the sending and receiving end voltages, respectively. Z and X are the series impedance and reactance of the line, respectively. The steady-state stability limit for the transmission line will be
Two wattmeter method is used for measurement of power in a balanced three-phase load supplied from a balanced three-phase system. If one of the wattmeter reads half of the other (both positive), then the power factor of the load is
A continuous-time input signal x (t ) is an eigen function of an LTI system, if the output is
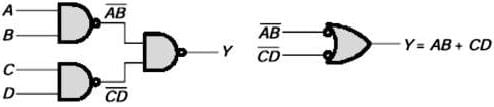
In the logic circuit shown in the figure, Y is given by
The value of the directional derivative of the function φ( x, y, z ) = xy2 + yz2 + zx2 at the point (2, -1, 1) in the direction of the vector p = i + 2 j +2k is
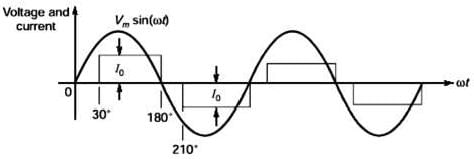
The waveform of the current drawn by a semi-converter from a sinusoidal AC voltage source is shown in the figure. If I0 = 20 A, the rms value of fundamental component of the current is __________ A (up to 2 decimal places).
The series impedance matrix of a short three-phase transmission line in phase coordinates is 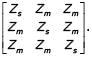 If the positive sequence impedance is (1 + j10)Ω, and the zero sequence is (4 + j31)Ω, then the imaginary part of Zm (in W) is __________ (up to 2 decimal places).
If the positive sequence impedance is (1 + j10)Ω, and the zero sequence is (4 + j31)Ω, then the imaginary part of Zm (in W) is __________ (up to 2 decimal places).
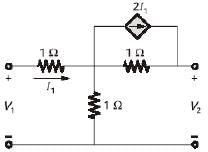
In the two-port network shown, the h11 parameter 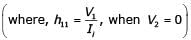 in ohms is ________ (up to 2 decimal places).
in ohms is ________ (up to 2 decimal places).
The graph of a network has 8 nodes and 5 independent loops. The number of branches of the graph is
In a salient pole synchronous motor, the developed reluctance torque attains the maximum value when the load angle in electrical degree is
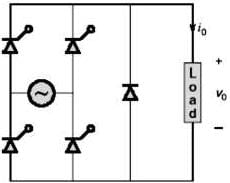
A single-phase fully controlled rectifier is supplying a load with an anti-parallel diode as shown in the figure. All switches and diodes are ideal. Which one of the following is true for instantaneous load voltage and current?
Let f be a real valued function of a real variable defined as 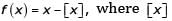 denotes the largest integer less than or equal to x. The value of
denotes the largest integer less than or equal to x. The value of 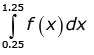 is ________ (up to 2 decimal places).
is ________ (up to 2 decimal places).
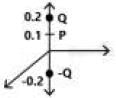
A positive charge of 1 nC is placed at (0, 0, 0.2) where all dimensions are in meters. Consider the x-y plane to be a conducting ground plane. Take 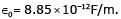 The Z component of the E field at (0, 0, 0.1) is closed to
The Z component of the E field at (0, 0, 0.1) is closed to
Consider a unity feedback system with forward transfer function given by
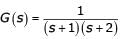
The steady-state error in the output of the system for a unit-step input is __________ (upto 2 decimal places).
Consider a non-singular 2 * 2 square matrix A. If trace ( A) = 4 and trace ( A2 ) = 5, the determinant of the matrix A is ________ (up 1 decimal place).
A 1000 * 1000 bus admittance matrix for an electric power system has 8000 non-zero elements. The minimum number of branches (transmission lines and transformers) in this system are ________ (upto 2 decimal places).
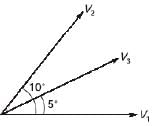
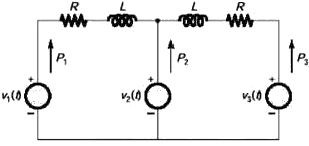
In the figure, the voltages are 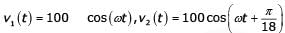 and
and 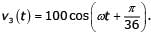 The circuit is in sinusoidal steady-state, and
The circuit is in sinusoidal steady-state, and 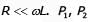 and P3 are the average power outputs. Which one of the following statements is true?
and P3 are the average power outputs. Which one of the following statements is true?
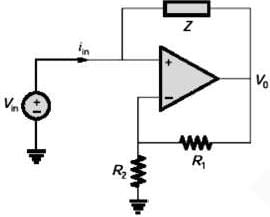
The op-amp shown in the figure is ideal. The input impedance is given by
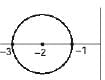
The value of the integral  in counter clockwise direction around a circle C of radius 1 with center at the point z =−2 is
in counter clockwise direction around a circle C of radius 1 with center at the point z =−2 is


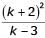 must be an integer, we can verify the options.
must be an integer, we can verify the options.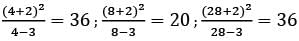

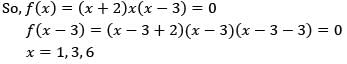
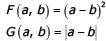
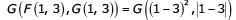
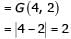
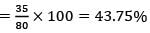

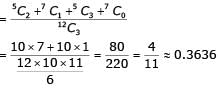
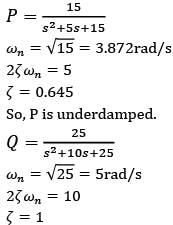
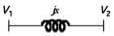
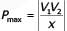
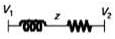
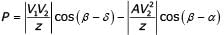
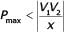
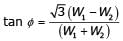
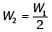
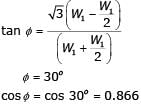
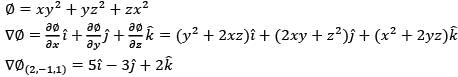
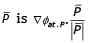
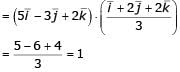
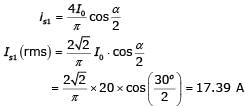
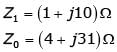
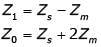
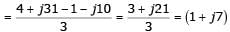
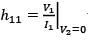 the equivalent circuit is given below.
the equivalent circuit is given below.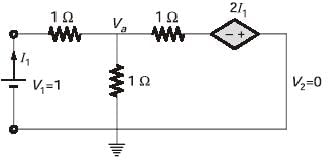
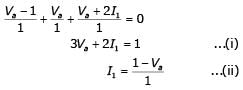
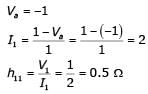
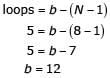
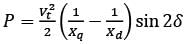
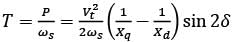
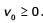
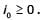
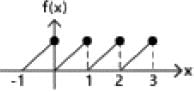
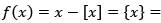 fractional part of x Graph of fractional part of x is given below.
fractional part of x Graph of fractional part of x is given below.