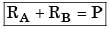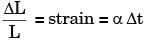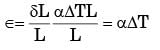Past Year Questions: Stress And Strain - Mechanical Engineering MCQ
23 Questions MCQ Test - Past Year Questions: Stress And Strain
Two identical circular rods of same diameter and same length are subjected to same magnitude of axial tensile force. One of the rods is made out of mild steel having the modulus of elasticity of 206 GPa. The other rod is made out of east iron having the modulus of elasticity of 100 GPa. Assume both the materials to be homogeneous and isotropic and the axial force causes the same amount of uniform stress in both the rods. The stresses developed are within the proportional limit of the respective materials. Which of the following observations is correct?
[2003]
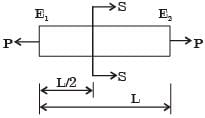
A rod of length L having uniform cross-section area A is subjected to a tensile force P as shown in the figure below. If the Young's modulus of the material varies linearly from E1 to E2 along the length of the rod, the normal stress developed at the section-SS at
[2013]

A thin plate of uniform thickness is subject to pressure as shown in the figure below
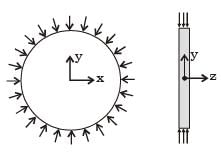
Under the assumption of plane stress, which one of the following is correct?
[2014]

Under the assumption of plane stress, which one of the following is correct?
The stress-strain curve for mild steel is shown in figure given below. Choose the correct option referring to both figure and table.
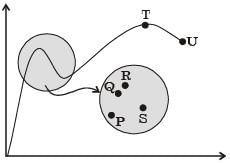
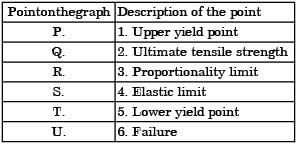
[2014]
Which one of the following types of stress-strain relationship best describes the behavior of brittle materials, such as ceramics and thermosetting plastics, (σ = stress and ε - strain)?
[2015]
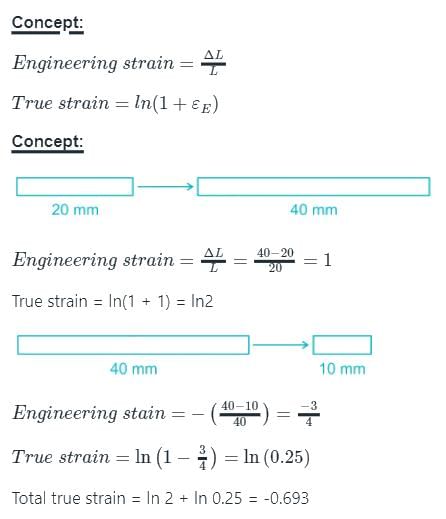
A rod of length 20 mm is stretched to make a rod of length 40 mm. Subsequently, it is compressed to make a rod of final length 10 mm. Consider the longitudinal tensile strain as positive and compressive strain as negative.The total true longitudinal strain in the rod is
[2017]
In the engineering stress-strain curve for mild steel, the Ultimate Tensile Strength (UTS) refers to
[2017]
The Poisson's ratio for a perfectly incompressible linear elastic material is
[2017]
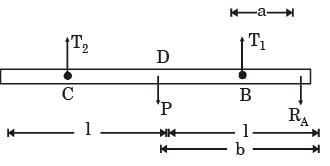
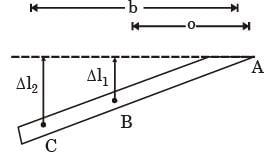
Below figure shows a rigid bar hinged at A and supported in a horizontal position by two vertical identical steel wires. Neglect the weight of the beam. The tension T1 and T2 induced in these wires by a vertical load P applied as shown are
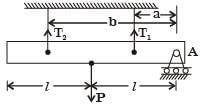
[1994]
In terms of Poisson's ratio (μ) the ratio of Young's modulus (E) to Shear modulus (G) of elastic materials is
[2004]
A 200 × 100 × 50 mm steel block is subjected to a hydrostatic pressure of 15 MPa. The Young's modulus and Poisson's ratio of the material are 200 GPa and 0.3 respectively. The change in the volume of the block in m3 is
[2007]
A rod of length L and diameter D is subjected to a tensile load P. Which of the following is sufficient to calculate the resulting change in diameter?
[2008]
A cylindrical container of radius R = 1 m, wall thickness 1 mm is filled with water up to a depth of 2 m and suspended along its upper rim. The density of water is 1000 kg/m3 and acceleration due to gravity is 10 m/s2. The self-weight of the cylinder is negligible. The formula for hoop stress in a thin-walled cylinder can be used at all points along the height of the cylindrical container.
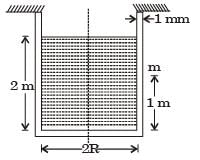
The axial and circumferential stress (σa, σc) experienced by the cylinder wall at mid-depth (m as shown) are
[2008]
A cylindrical container of radius R = 1 m, wall thickness 1 mm is filled with water up to a depth of 2 m and suspended along its upper rim. The density of water is 1000 kg/m3 and acceleration due to gravity is 10 m/s2. The self-weight of the cylinder is negligible. The formula for hoop stress in a thin-walled cylinder can be used at all points along the height of the cylindrical container.
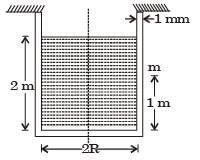
If the Young's modulus and Poisson's ratio of the container material' are 100 GPa and 0.3, respectively, the axial strain in the cylinder wall at mid-depth is
[2008]
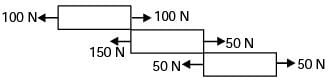
The figure below shows a steel rod of 25 mm2 cross sectional area. It is loaded at four points. K, L, M and N. Assume Esteel = 200 GPa. The total change in length of the rod due to loading is

[2004]
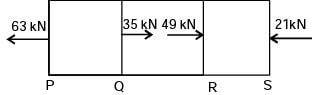
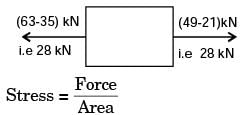
A bar having a cross-sectional area of 700 mm2 is subjected to axial loads at the positions indicated. The value of stress in the segment QR is

[2006]
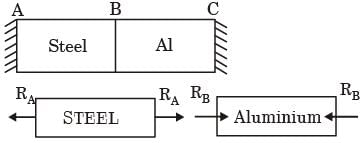
A bimetallic cylindrical bar of cross sectional area 1 m2 is made by bonding Steel (Young's modulus = 210 GPa) and Aluminium (Young's modulus = 70 GPa) as shown in the figure. To maintain tensile axial strain of magnitude 10–6 in steel bar and compressive axial strain of magnitude 10–6 in Aluminum bar, the magnitude of the required force P(in kN) along the indicated direction is
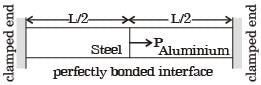
[2018]
A free bar of length / is uniformly heated from 0°C to a temperature t°C, α is the coefficient of linear expansion and E the modulus of elasticity. The stress in the bar is
[1995]
A uniform, slender cylindrical rod is made of a homogeneous and isotropic material. The rod rests on a frictionless surface. The rod is heated uniformly. If the radial and longitudinal thermal stresses are represented by σr and σz respectively, then
[2005]
A steel rod of length L and diameter D, fixed at both ends, is uniformly heated to a temperature rise of ΔT. The Young's modulus is E and the coefficient of linear expansion is a. The thermal stress in the rod is
[2007]
A solid steel cube constrained on all six faces is heated so that the temperature rises uniformly by ΔT. If the thermal coefficient of the material is α, Young's modulus is E and the Poisson's ratio is v , the thermal stress developed in the cube due to heating is
[2012]
A circular rod of length L and area of crosssection A has a modulus of elasticity E and coefficient of thermal expansion α. One end of the rod is fixed and other end is free. If the temperature of the rod is increased by ΔT, then
[2014]
A steel cube, with all faces free to deform, has Young's modulus, E, Poisson's ratio, v, and coefficient of thermal expansion, a. The pressure (hydrostatic stress) developed within the cube, when it is subjected to a uniform increase in temperature, ΔT, is given by
[2014]


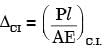
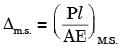



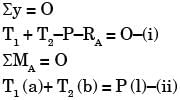
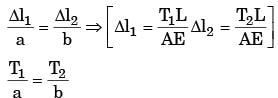
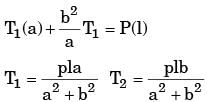
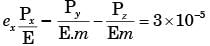
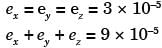

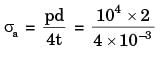
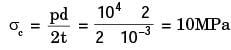
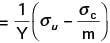
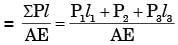
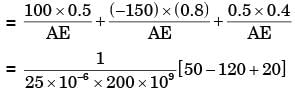 = –1 × 10–5 m = –10μm
= –1 × 10–5 m = –10μm